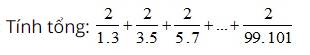\(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{99\cdot101}\\ =1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\\ =1-\dfrac{1}{101}=\dfrac{100}{101}\)
\(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{99.101}.\\= \dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}.\\ =\dfrac{1}{1}+\left(-\dfrac{1}{3}+\dfrac{1}{3}\right)+\left(-\dfrac{1}{5}+\dfrac{1}{5}\right)+...+\left(-\dfrac{1}{99}+\dfrac{1}{99}\right)-\dfrac{1}{101}.\\ =\dfrac{1}{1}+0+0+...+0-\dfrac{1}{101}.\\ =1-\dfrac{1}{101}=\dfrac{100}{101}.\)