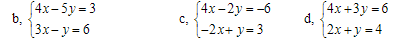b: \(\Leftrightarrow\left\{{}\begin{matrix}4x-5y=3\\15x-5y=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-11y=-27\\3x-y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{27}{11}\\3x=y+6=\dfrac{27}{11}+6=\dfrac{93}{11}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{31}{11}\\y=\dfrac{27}{11}\end{matrix}\right.\)
c: \(\Leftrightarrow\left\{{}\begin{matrix}2x-y=-3\\2x-y=-3\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in R\)
d: \(\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\4x+8y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-5y=-10\\2x+y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)
\(b\)
\(\begin{cases} 4x-5y=3\\3x-y=6 \end{cases}\)
\(\Leftrightarrow \begin{cases} 4x-5y=3\\15x-5y=30 \end{cases}\)
\(\Leftrightarrow \begin{cases}y=3x-6\\15x-5y-4x+5y=30-3\end{cases}\)
\(\Leftrightarrow \begin{cases}y=3x-6\\11x=27\end{cases}\)
\(\Leftrightarrow \begin{cases}y=\dfrac{15}{11}\\x=\dfrac{27}{11}\end{cases}\)
Vậy ` (x;y)=(27/11;15/11) `