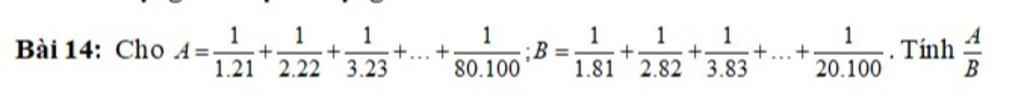\(A=\dfrac{1}{1\cdot21}+\dfrac{1}{2\cdot22}+\dfrac{1}{3\cdot23}+...+\dfrac{1}{80\cdot100}\)
\(A=1\cdot\dfrac{1}{21}+\dfrac{1}{2}\cdot\dfrac{1}{22}+...+\dfrac{1}{80}\cdot\dfrac{1}{100}\)
\(A=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{80}\right)-\left(\dfrac{1}{21}+\dfrac{1}{22}+\dfrac{1}{23}+...+\dfrac{1}{100}\right)\)
\(A=1-\left(\dfrac{1}{\left(80-2\right)+1}\right)-\left(\dfrac{1}{\left(100-22\right)+1}\right)\)
\(A=1-\dfrac{1}{79}-\dfrac{1}{79}\)
\(A=1\)
Ta có: A=1.
\(B=\dfrac{1}{1\cdot81}+\dfrac{1}{2\cdot82}+\dfrac{1}{3\cdot83}+...+\dfrac{1}{20\cdot100}\)
\(B=1\cdot\dfrac{1}{81}+\dfrac{1}{2}\cdot\dfrac{1}{82}+\dfrac{1}{3}\cdot\dfrac{1}{83}+...+\dfrac{1}{20}\cdot\dfrac{1}{100}\)
\(B=1-\left(\dfrac{1}{1}+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{20}\right)-\left(\dfrac{1}{81}+\dfrac{1}{82}+\dfrac{1}{83}+...+\dfrac{1}{100}\right)\)
\(B=1-\left(\dfrac{1}{\left(20-1\right)+1}\right)-\left(\dfrac{1}{\left(100-81\right)+1}\right)\)
\(B=1-\dfrac{1}{20}-\dfrac{1}{20}\)
\(B=1\)
\(\Rightarrow\) Ta có tỉ số của \(\dfrac{A}{B}=1\)