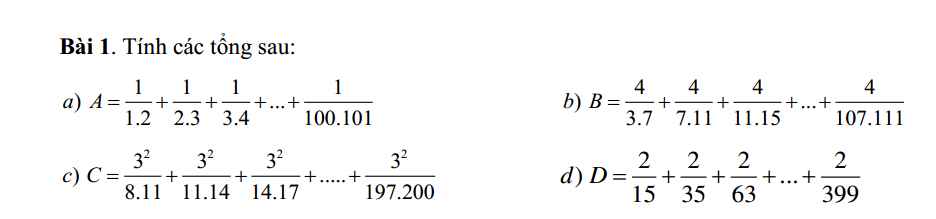a) \(A=\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{100.101}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{100}-\dfrac{1}{101}\)
\(=1-\dfrac{1}{101}=\dfrac{100}{101}\)
b) \(B=\dfrac{4}{3.7}+\dfrac{4}{7.11}+...+\dfrac{4}{107.111}\)
\(=\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+...+\dfrac{1}{107}-\dfrac{1}{111}\)
\(=\dfrac{1}{3}-\dfrac{1}{111}=\dfrac{12}{37}\)
c) \(C=\dfrac{3^2}{8.11}+\dfrac{3^2}{11.14}+...+\dfrac{3^2}{197.200}\)
\(=3\left(\dfrac{3}{8.11}+\dfrac{3}{11.14}+...+\dfrac{3}{197.200}\right)\)
\(=3\left(\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}+...+\dfrac{1}{197}-\dfrac{1}{200}\right)\)
\(=3\left(\dfrac{1}{8}-\dfrac{1}{200}\right)=3.\dfrac{3}{25}=\dfrac{9}{25}\)
d) \(D=\dfrac{2}{15}+\dfrac{2}{35}+...+\dfrac{2}{399}\)
\(=\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{19.21}\)
\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{19}-\dfrac{1}{21}\)
\(=\dfrac{1}{3}-\dfrac{1}{21}=\dfrac{2}{7}\)