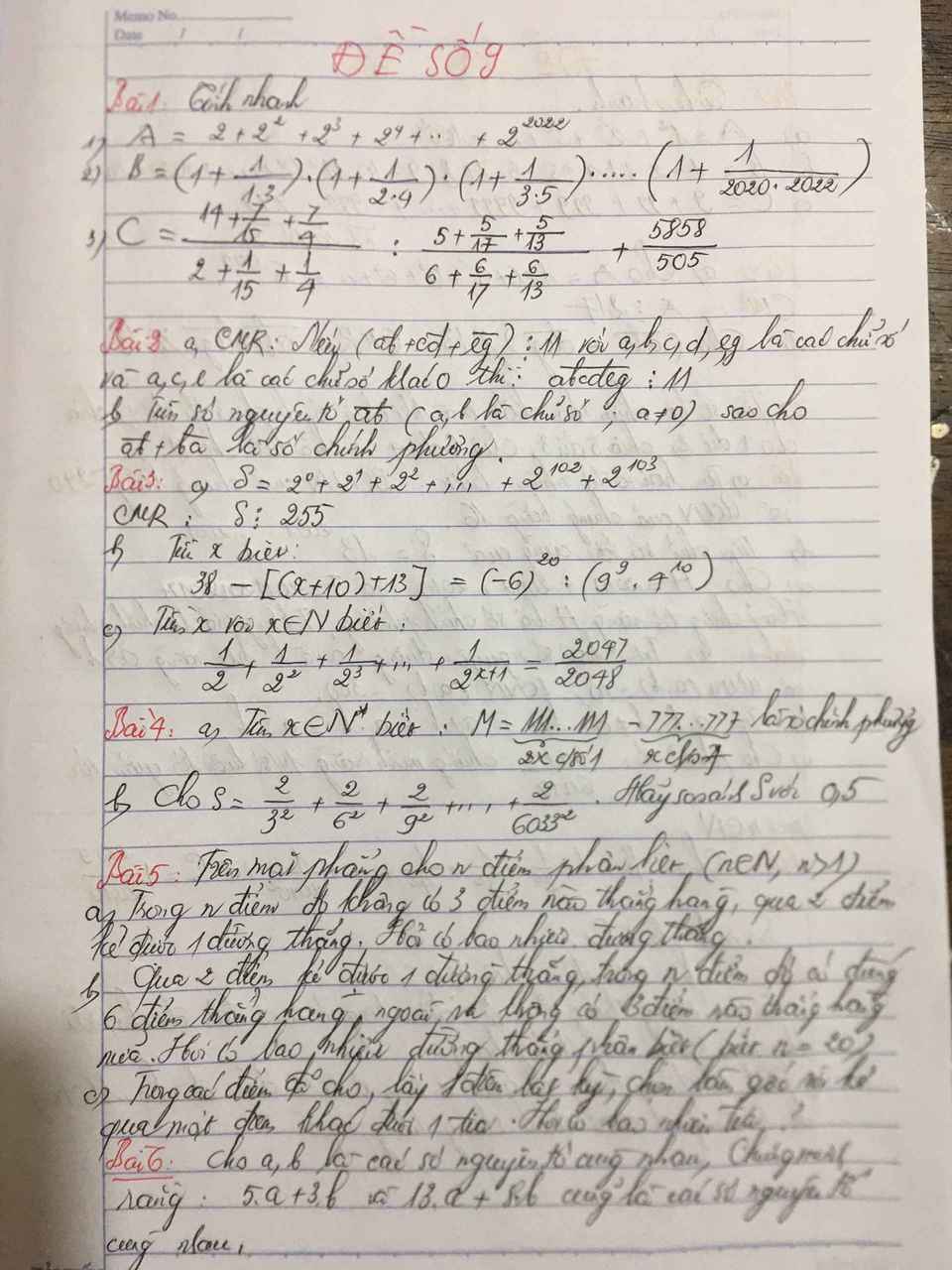\(B=\left(1+\dfrac{1}{1.3}\right)\left(1+\dfrac{1}{2.4}\right)\left(1+\dfrac{1}{3.5}\right).....\left(1+\dfrac{1}{2020.2022}\right)\)
\(=\dfrac{1.3+1}{1.3}.\dfrac{2.4+1}{2.4}.\dfrac{3.5+1}{3.5}....\dfrac{2020.2022+1}{2020.2022}\)
\(=\dfrac{2^2}{1.3}.\dfrac{3^2}{2.4}.\dfrac{4^2}{3.5}.....\dfrac{2021^2}{2020.2022}\)
\(=\dfrac{2.2021}{2022}=\dfrac{4042}{2022}\)
\(C=\dfrac{14+\dfrac{7}{15}+\dfrac{7}{4}}{2+\dfrac{1}{15}+\dfrac{1}{4}}:\dfrac{5+\dfrac{5}{17}+\dfrac{5}{13}}{6+\dfrac{6}{17}+\dfrac{6}{13}}+\dfrac{5858}{5050}\)
\(=\dfrac{7\left(2+\dfrac{1}{15}+\dfrac{1}{4}\right)}{2+\dfrac{1}{15}+\dfrac{1}{4}}:\dfrac{5\left(1+\dfrac{1}{17}+\dfrac{1}{13}\right)}{6\left(1+\dfrac{1}{17}+\dfrac{1}{13}\right)}+\dfrac{58}{50}\)
\(=7:\dfrac{5}{6}+\dfrac{29}{25}=7.\dfrac{6}{5}+\dfrac{29}{25}\)
\(=\dfrac{42}{5}+\dfrac{29}{25}=\dfrac{239}{25}\)