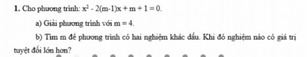a) Thay m = 4 vào phương trình, ta có:
x2 - 6x + 5 = 0
<=> (x2-x) - (5x-5) = 0
<=> x(x-1) - 5(x-1) = 0
<=> (x-5)(x-1) = 0
<=> \(\left\{{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)
KL: Phương trình có tập nghiệm S = {1;5}
b)
Xét \(\Delta'=\left[-\left(m-1\right)\right]^2-1.\left(m+1\right)\)
= \(m^2-2m+1-m-1=m^2-3m=m\left(m-3\right)\)
Phương trình có 2 nghiệm phân biệt <=> \(m\left(m-3\right)>0\Leftrightarrow\left[{}\begin{matrix}m>3\\m< 0\end{matrix}\right.\)
Theo định lý Vi-ét, ta có \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2m-2}{1}=2m-2\\x_1.x_2=\dfrac{m+1}{1}=m+1\end{matrix}\right.\)
Phương trình có 2 nghiệm trái dấu
<=> x1.x2 < 0
<=> m + 1 < 0
<=> m < -1 (T/m)
Với m < -1 <=> 2m-2 < -4
=> \(x_1+x_2< 0\)
=> Nghiệm âm có giá trị tuyệt đối lớn hơn
a) Thay m = 4 vào phương trình, ta có:
x2 - 6x + 5 = 0
<=> (x2-x) - (5x-5) = 0
<=> x(x-1) - 5(x-1) = 0
<=> (x-5)(x-1) = 0
<=> {x=5x=1{x=5x=1
KL: Phương trình có tập nghiệm S = {1;5}
b)
Xét Δ′=[−(m−1)]2−1.(m+1)Δ′=[−(m−1)]2−1.(m+1)
= m2−2m+1−m−1=m2−3m=m(m−3)m2−2m+1−m−1=m2−3m=m(m−3)
Phương trình có 2 nghiệm phân biệt <=> m(m−3)>0⇔[m>3m<0m(m−3)>0⇔[m>3m<0
Theo định lý Vi-ét, ta có