\(g'\left(x\right)=-x^2+\left(2m+3\right)x-\left(m^2+3m\right)\)
\(g'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=m\\x=m+3\end{matrix}\right.\)
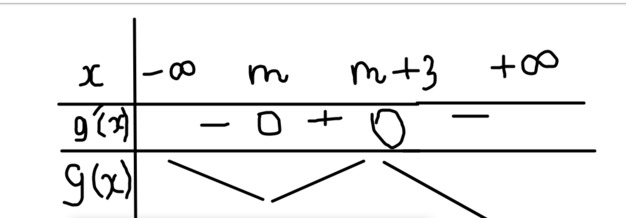
\(\left|g\left(x\right)\right|nb/\left(1;2\right)\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}g'\left(x\right)\ge0,\forall x\in\left(1;2\right)\\g\left(x\right)\le0,\forall x\in\left(1;2\right)\end{matrix}\right.\\\left\{{}\begin{matrix}g'\left(x\right)\le0,\forall x\in\left(1;2\right)\\g\left(x\right)\ge0,\forall x\in\left(1;2\right)\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}m\le1< 2\le m+3\\g\left(2\right)\le0\end{matrix}\right.\\\left\{{}\begin{matrix}m+3\le1\\g\left(2\right)\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}2\le m\\g\left(2\right)\ge0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-1\le m\le1\\-2m^2-2m+4\le0\end{matrix}\right.\\\left\{{}\begin{matrix}m\le-2\\-2m^2-2m+4\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}m\ge2\\-2m^2-2m+4\ge0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-1\le m\le1\\m\in(-\infty;-2]\cup[1;+\infty)\end{matrix}\right.\\\left\{{}\begin{matrix}m\le-2\\m\in\left[-2;1\right]\end{matrix}\right.\\\left\{{}\begin{matrix}m\ge2\\m\in\left[-2;1\right]\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-2\\m=1\end{matrix}\right.\) \(\Rightarrow m\in\left\{-2;1\right\}\)
Có 2 giá trị m thỏa mãn










