Nhận xét: Ta thấy cách vẽ đồ thị của hàm số \(y=\left|x^3-3x^2-ax+a\right|\) bằng cách giữ nguyên phần đồ thị hàm \(f\left(x\right)=x^3-3x^2-ax+a\) ở phía trên Ox rồi lấy đối xứng phần đồ thị ở dưới Ox .
Nên để ..... đồng biến trên \(\left(0;+\infty\right)\) khi và chỉ khi pt \(x^3-3x^2-ax+a=0\) ko có nghiệm nào lớn hơn 0 \(\left(x\in(-\infty;0]\right)\)
\(x^3-3x^2-ax+a=0\Leftrightarrow a\left(x-1\right)=x^3-3x^2\Leftrightarrow a=\dfrac{x^3-3x^2}{x-1}=g\left(x\right)\)
Xét hàm g(x) trên \(R\backslash\left\{1\right\}\)
\(g'\left(x\right)=\dfrac{2x^3-6x^2+6x}{\left(x-1\right)^2}\);\(g'\left(x\right)=0\Leftrightarrow x=0\)
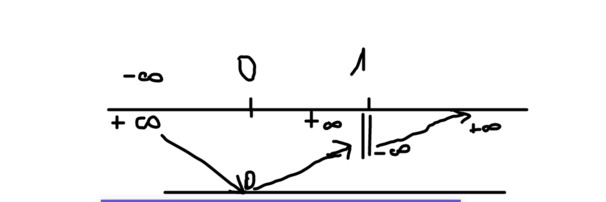
Để ko có nghiệm nào vượt quá 0\(\Leftrightarrow a\le0\) => vo so










