Phác thảo nhanh dạng đồ thị của \(t=\left|x^3\right|-3x^2+1\)
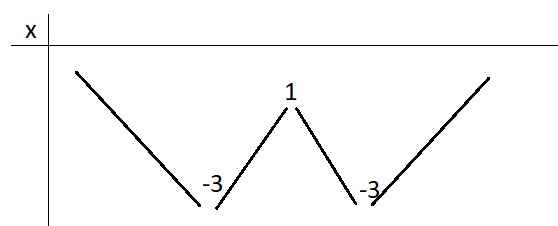
Từ đây ta thấy:
\(t=-3\) hoặc \(t>1\) cho 2 nghiệm x
\(t=1\) cho 3 nghiệm x
\(-3< t< 1\) cho 4 nghiệm x
Đồng thời từ đồ thị hàm đề bài ta thấy: \(f\left(t\right)=k\) (với \(t\ge-3\)) thì:
\(k=f_{CT}\) cho 2 nghiệm \(\left\{{}\begin{matrix}t=-3\\t=-4>1\end{matrix}\right.\) \(\Rightarrow2+2=4\) nghiệm x (ktm)
\(f_{CT}< k< 0\) cho 3 nghiệm: \(\left\{{}\begin{matrix}-3< t< -2\\t>1\\t>1\end{matrix}\right.\) cho \(4+2+2=8\) nghiệm x (thỏa)
\(k=0\Rightarrow\left\{{}\begin{matrix}t=-2\in\left(-3;1\right)\\t=1\\t>1\end{matrix}\right.\) cho \(4+3+2=9\) nghiệm x (ktm)
\(0< k< f_{CĐ}\) \(\Rightarrow\left\{{}\begin{matrix}t\in\left(-3;1\right)\\t\in\left(-3;1\right)\\t>1\end{matrix}\right.\) \(\Rightarrow4+4+2=10\) nghiệm x
\(k>f_{CĐ}\Rightarrow t>1\Rightarrow2\) nghiệm x
Vậy pt có 8 nghiệm thực khi: \(f_{CT}< f\left(\dfrac{m-1}{2}\right)< 0\)
\(\Rightarrow\left[{}\begin{matrix}-3< \dfrac{m-1}{2}< -2\\1< \dfrac{m-1}{2}< 6\\\dfrac{m-1}{2}\ne4\end{matrix}\right.\) \(\Rightarrow m\)










