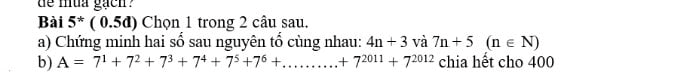a) Gọi d là UCLN(4n+3;7n+5)
\(\Rightarrow\left\{{}\begin{matrix}4n+3⋮d\\7n+5⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}28n+21⋮d\\28n+20⋮d\end{matrix}\right.\)
\(\Rightarrow\left(28n+21\right)-\left(28n+20\right)⋮d\Rightarrow1⋮d\)
Vậy 4n+3 và 7n+5 là 2 số nguyên tố cùng nhau
b) \(A=7\left(1+7+7^2+7^3\right)+7^5\left(1+7+7^2+7^3\right)+...+7^{2009}\left(1+7+7^2+7^3\right)\)
\(=7.400+7^5.400+...+7^{2009}.400=400\left(7+7^5+...+7^{2009}\right)⋮400\)
Đúng 0
Bình luận (0)
