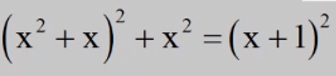Pt\(\Leftrightarrow x^2\left(x+1\right)^2+x^2-\left(x+1\right)^2=0\)
Đặt \(\left\{{}\begin{matrix}a=x\\b=x+1\end{matrix}\right.\Rightarrow b-a=1\)
Ta lập được hpt:
\(\left\{{}\begin{matrix}a^2b^2+a^2-b^2=0\\b-a=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b^2+\left(a-b\right)\left(a+b\right)=0\\b-a=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2\left(a+1\right)^2-a-\left(a+1\right)=0\left(\cdot\right)\\b=a+1\end{matrix}\right.\)
\(\left(\cdot\right)\Leftrightarrow a^2\left(a+1\right)^2=1\Leftrightarrow\left[{}\begin{matrix}a^2+a=1\\a^2+a=-1\end{matrix}\right.\Leftrightarrow a^2+a-1=0\Leftrightarrow\left[{}\begin{matrix}a=\dfrac{-1+\sqrt{5}}{2}\\a=\dfrac{-1-\sqrt{5}}{2}\end{matrix}\right.\)
Từ đó kết luận nghiệ, của pt