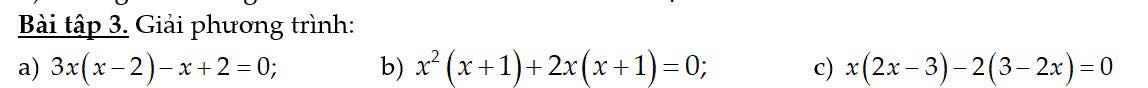Question

 

Answer 1

a. 3x(x - 2) - x + 2 = 0

<=> 3x² - 6x - x + 2 = 0

<=> 3x² - 7x + 2 = 0

<=> 3x² - 6x - x + 2 = 0

<=> 3x(x - 2) - (x - 2) = 0

<=> (3x - 1)(x - 2) = 0

<=> \(\left[{}\begin{matrix}3x-1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=2\end{matrix}\right.\)

b. x²(x + 1) + 2x(x + 1) = 0

<=> (x² + 2x)(x + 1) = 0

<=> x(x + 2)(x + 1) = 0

<=> \(\left[{}\begin{matrix}x=0\\x+2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=-1\end{matrix}\right.\)

c. x(2x - 3) - 2(3 - 2x) = 0

<=> x(2x - 3) + 2(2x - 3) = 0

<=> (x + 2)(2x - 3) = 0

<=> \(\left[{}\begin{matrix}x+2=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{3}{2}\end{matrix}\right.\)