\(\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{8.9}+\dfrac{1}{9.10}\right).100-\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right]:\dfrac{1}{2}=89\)
\(\Leftrightarrow\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\right).100-2\left(\dfrac{5}{2}.\dfrac{100}{100x+206}\right)=89\)
\(\Leftrightarrow\left(1-\dfrac{1}{10}\right).100-2.\dfrac{125}{50x+103}=89\)
\(\Leftrightarrow90-\dfrac{250}{50x+103}=89\)
\(\Leftrightarrow\dfrac{250}{50x+103}=1\)
\(\Leftrightarrow250=50x+103\Leftrightarrow50x=147\Leftrightarrow x=\dfrac{147}{50}\)
Ta có: \(\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{8\cdot9}+\dfrac{1}{9\cdot10}\right)\cdot100-\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right]:\dfrac{1}{2}=89\)
\(\Leftrightarrow\left(1-\dfrac{1}{10}\right)\cdot100-\left[\dfrac{5}{2}:\left(x+\dfrac{103}{50}\right)\right]:\dfrac{1}{2}=89\)
\(\Leftrightarrow\left[\dfrac{5}{2}:\left(x+\dfrac{103}{50}\right)\right]:\dfrac{1}{2}=1\)
\(\Leftrightarrow\dfrac{5}{2}:\left(x+\dfrac{103}{50}\right)=2\)
\(\Leftrightarrow x+\dfrac{103}{50}=\dfrac{5}{4}\)
hay \(x=-\dfrac{81}{100}\)

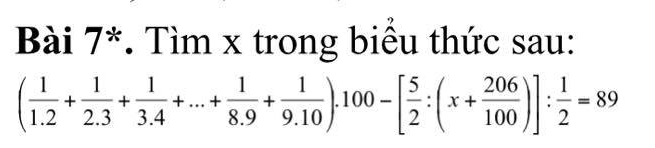










 4 và 5
4 và 5



