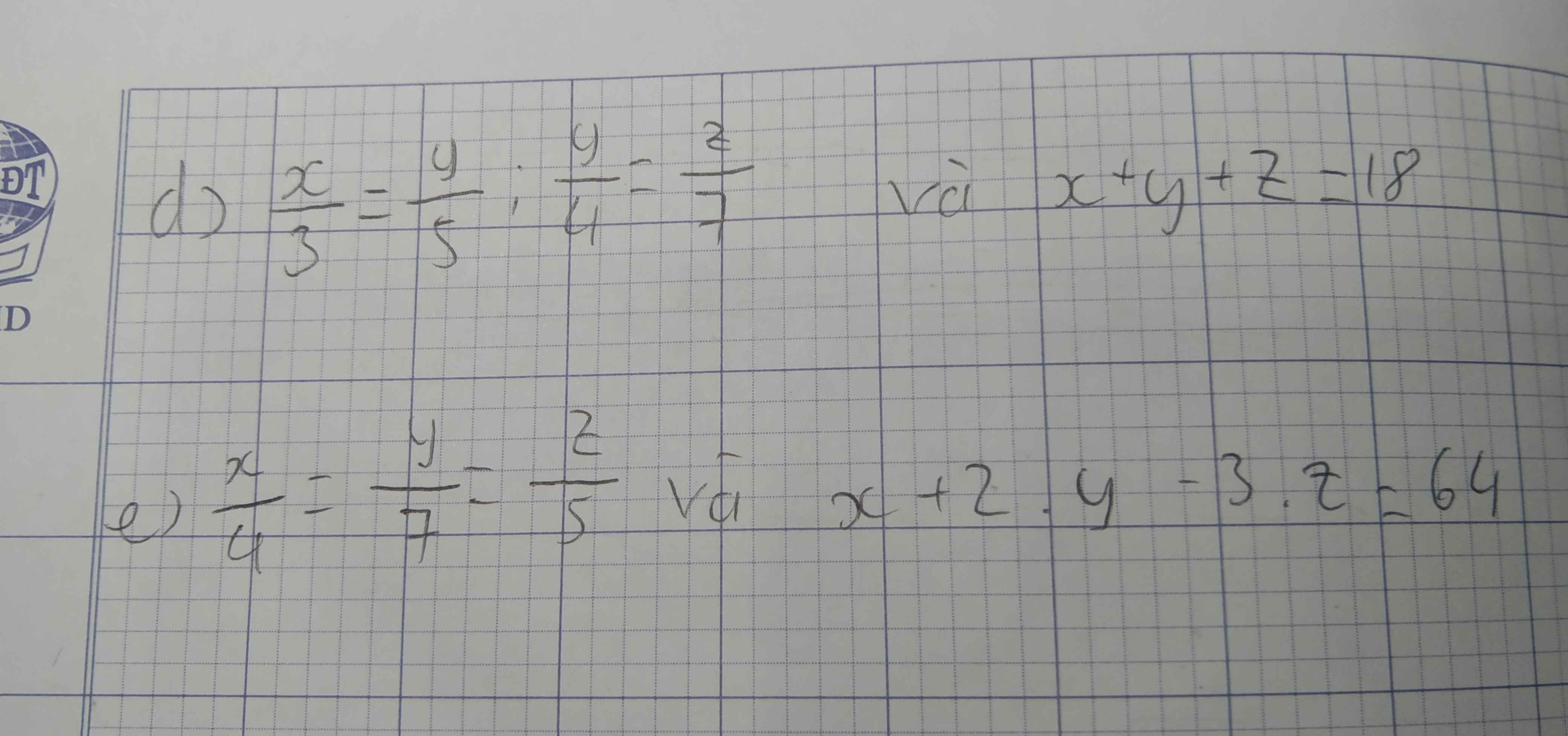\(\dfrac{x}{3}=\dfrac{y}{5}=>x=\dfrac{3y}{5}\)
\(\dfrac{y}{4}=\dfrac{z}{7}\)\(=>z=\dfrac{7y}{4}\)
\(=>x+y+z=\dfrac{3y}{5}+y+\dfrac{7y}{4}=18=>\dfrac{12y+20y+35y}{20}=18\)
\(=>\dfrac{67y}{20}=18=>y=\dfrac{360}{67}=>x=\dfrac{3.\dfrac{360}{67}}{5}=\dfrac{216}{67},z=\dfrac{7.\dfrac{360}{67}}{4}=\dfrac{630}{67}\)
e,
\(=>\dfrac{x}{4}=\dfrac{y}{7}=>x=\dfrac{4y}{7}\)
\(\dfrac{y}{7}=\dfrac{z}{5}=>z=\dfrac{5y}{7}\)
rồi thế x,z vào x+2y-3z=64 tính được y rồi tìm đc x,z tương tự ý d