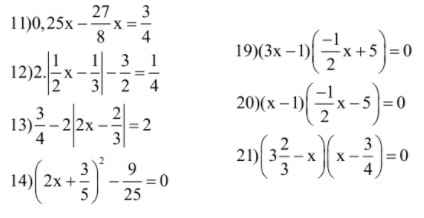14) Ta có: \(\left(2x+\dfrac{3}{5}\right)^2-\dfrac{9}{25}=0\)
\(\Leftrightarrow\left(2x+\dfrac{3}{5}\right)^2=\dfrac{9}{25}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{3}{5}=\dfrac{3}{5}\\2x+\dfrac{3}{5}=-\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=0\\2x=-\dfrac{6}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{3}{5}\end{matrix}\right.\)
Vậy: \(x\in\left\{0;-\dfrac{3}{5}\right\}\)
19) Ta có: \(\left(3x-1\right)\left(-\dfrac{1}{2}x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\-\dfrac{1}{2}x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=1\\-\dfrac{1}{2}x=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=10\end{matrix}\right.\)
Vậy: \(x\in\left\{\dfrac{1}{3};10\right\}\)
20) Ta có: \(\left(x-1\right)\left(-\dfrac{1}{2}x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\-\dfrac{1}{2}x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\-\dfrac{1}{2}x=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-10\end{matrix}\right.\)
Vậy: \(x\in\left\{1;-10\right\}\)
21) Ta có: \(\left(3\dfrac{2}{3}-x\right)\left(x-\dfrac{3}{4}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{3}\\x=\dfrac{3}{4}\end{matrix}\right.\)
Vậy: \(x\in\left\{\dfrac{11}{3};\dfrac{3}{4}\right\}\)
11) PT \(\Rightarrow-\dfrac{25}{8}x=\dfrac{3}{4}\) \(\Rightarrow x=-\dfrac{6}{25}\)
Vậy ...
12) PT \(\Rightarrow\left|\dfrac{1}{2}x-\dfrac{1}{3}\right|=\dfrac{7}{8}\) \(\Rightarrow\left[{}\begin{matrix}\dfrac{1}{2}x-\dfrac{1}{3}=\dfrac{7}{8}\\\dfrac{1}{3}-\dfrac{1}{2}x=\dfrac{7}{8}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{29}{12}\\x=-\dfrac{13}{48}\end{matrix}\right.\)
Vậy ...
13) PT \(\Rightarrow\left|2x-\dfrac{2}{3}\right|=-\dfrac{5}{8}\) (Vô lý)
Vậy phương trình vô nghiệm