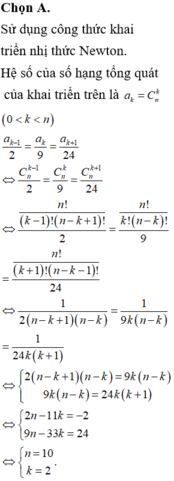Các câu hỏi tương tự
Cho
n
∈
N
*
và
1
+
x
n
a
0
+
a
1
x
+
.
.
.
+
a
n
x
n
. Biết rằng tồn tại số nguyên
k
1
≤...
Đọc tiếp
Cho n ∈ N * và 1 + x n = a 0 + a 1 x + . . . + a n x n . Biết rằng tồn tại số nguyên k 1 ≤ k ≤ n - 1 sao cho a k - 1 2 = a k 9 = a k + 1 24 . Tính n?
A. 10
B. 11
C. 20
D. 22
Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:A(n) : “nếu a và b là những số nguyên dương mà max{a,b} n thì a b”Chứng minh :Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} 1 thì a b”Mệnh đề A(1) đúng vì max{a,b} 1 và a,b là những số nguyên dương thì a b 1.Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1Bước 3: xét max{a,b} k+1 ⇒max{a-1,b-1} k+ 1-1 kDo a(k) là mệnh đề đúng nên a- 1 b-1 ⇒ a b⇒...
Đọc tiếp
Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?
Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:
A(n) : “nếu a và b là những số nguyên dương mà max{a,b} = n thì a = b”
Chứng minh :
Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} = 1 thì a = b”
Mệnh đề A(1) đúng vì max{a,b} = 1 và a,b là những số nguyên dương thì a= b =1.
Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1
Bước 3: xét max{a,b} = k+1 ⇒max{a-1,b-1} = k+ 1-1 = k
Do a(k) là mệnh đề đúng nên a- 1= b-1 ⇒ a= b⇒ A(k+1) đúng.
Vậy A(n) đúng với mọi n ∈N*
A. Bước 1
B. Bước 2
C. Bước 3
D. Không có bước nào sai
Cho khai triển
1
+
2
x
n
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
n...
Đọc tiếp
Cho khai triển 1 + 2 x n = a 0 + a 1 x + a 2 x 2 + . . . + a n x n , n ≥ 1. Tìm số giá trị nguyên của n với n ≤ 2018 sao cho tồn tại k 0 ≤ k ≤ n - 1 thỏa mãn a k = a k + 1
A. 2018
B. 673
C. 672
D. 2017
Tập hợp A gồm n phần tử
n
≥
4
. Biết rằng số tập hợp con chứa 4 phần tử của A bằng 20 lần số tập hợp con chứa 2 phần tử của A. Tìm số
k
∈
1
;
2
;
.
.
.
;
n
sao cho số tập hợp con chứa k phần tử của A là lớn nhất. A. 9...
Đọc tiếp
Tập hợp A gồm n phần tử n ≥ 4 . Biết rằng số tập hợp con chứa 4 phần tử của A bằng 20 lần số tập hợp con chứa 2 phần tử của A. Tìm số k ∈ 1 ; 2 ; . . . ; n sao cho số tập hợp con chứa k phần tử của A là lớn nhất.
A. 9
B. 8
C. 7
D. 6
1) biết các nghiệm của phương trình \(cos2x=-\dfrac{1}{2}\) có dạng \(x=\dfrac{\pi}{m}+k\pi,k\in Z\) với m,n là các số nguyên dương. Khi đó m+n bằng
2) cho \(x=\dfrac{\pi}{3}+k2\pi\left(k\in Z\right)\) là nghiệm của phương trình
3) cho \(x=\dfrac{\pi}{2}+k\pi\left(k\in Z\right)\) là nghiệm của phương trình
Cho tập hợp A có n phần tử
(
n
≥
4
)
. Biết rằng số tập con của A có 8 phần tử nhiều gấp 26 lần số tập con của A có 4 phần tử. Hãy tìm
k
∈
1
,
2
,
3...
Đọc tiếp
Cho tập hợp A có n phần tử ( n ≥ 4 ) . Biết rằng số tập con của A có 8 phần tử nhiều gấp 26 lần số tập con của A có 4 phần tử. Hãy tìm k ∈ 1 , 2 , 3 , . . . , n sao cho số tập con gồm k phần tử của A là nhiều nhất
A. k = 20
B. k = 11
C. k = 14
D. k = 10
tìm tất cả các bộ (n,k,p), với n,k là các số nguyên lớn hơn 1 và p là 1 số nguyên tố thỏa mãn \(n^5+n^4-2n^3-2n^2+1=p^k\)
tìm tất cả các bộ (n,k,p), với n,k là các số nguyên lớn hơn 1 và p là 1 số nguyên tố thỏa mãn \(n^5+n^4-2n^3-2n^2+1=p^k\)
Giá trị của k để hàm só f(x)=\(\hept{\begin{cases}\frac{x^{2019}+x-2}{\sqrt{2020+1}-\sqrt{x+2020}}\\2k\end{cases}}\) liên tục tại x0=1 có dạng \(k=\frac{a\sqrt{b}}{c}\), với a,b,c là các số nguyên và \(\frac{a\sqrt{b}}{c}\)
là phân số tới giản. tính a-b+c ( f(x) = 2k , khi x<=1; f(x)=... khi x>1)