Cho hình chóp S. ABCD có đáy là hình thang (AB// CD). Tìm khẳng định sai?
A. Hình chóp có 4 mặt bên.
B. Giao tuyến của mặt phẳng (SAC) và (SBD) là SO. ( O là giao điểm của AC và BD).
C. Giao tuyến của mặt phẳng (SAD) và ( SBD) là SI ( I là giao điểm của AD và BC).
D. Giao tuyến của mặt phẳng (SAB) và (SAD) là đường trung bình của hình thang ABCD
Chọn D
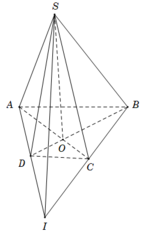
+Hình chóp S. ABCD có 4 mặt bên là (SAB); (SBC) ; (SCD) và (SAD): Do đó A đúng.
+ S là điểm chung thứ nhất của hai mặt phẳng (SAC) và (SBD)
là điểm chung thứ hai của hai mặt phẳng (SAC) và (SBD)
O ∈ A C ⊂ S A C ⇒ O ∈ S A C O ∈ B D ⊂ S B D ⇒ O ∈ S B D ⇒ O
=> giao tuyến của ( SAC) và (SBD) là SO.
Do đó B đúng.
+ Tương tự, ta có giao tuyến của mặt phẳng (SAD) và ( SBD) là SI ( I là giao điểm của AD và BC). Do đó C đúng.
+ giao tuyến của ( SAB) và (SAD) là SA mà SA không phải là đường trung bình của hình thang ABCD.
Do đó D sai.




