Các câu hỏi tương tự
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
(
x
-
1
)
2
(
x
-
2
)
. Hỏi hàm số
y
f
5
x
x
2
+
4...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x ( x - 1 ) 2 ( x - 2 ) . Hỏi hàm số y = f 5 x x 2 + 4 đồng biến trên khoảng nào dưới đây ?
A. ( - ∞ ; - 2 ) .
B. (0;2).
C. (2;4).
D. (-2;1)
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
2
(
x
-
1
)
(
x
-
4
)
g
(
x
)
, trong đó
g
(
x
)
0
,
∀
x
. Hàm số
y
f
(
x
2...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) ( x - 4 ) g ( x ) , trong đó g ( x ) > 0 , ∀ x . Hàm số y = f ( x 2 ) đồng biến trên khoảng nào dưới đây?
A. ( - ∞ ; - 2 ) .
B. (-1;1).
C. (-2;-1).
D. (1;2).
Cho hàm số y f(x) có
f
(
x
)
(
x
-
2
)
(
x
+
5
)
(
x
+
1
)
....
Đọc tiếp
Cho hàm số y = f(x) có f ' ( x ) = ( x - 2 ) ( x + 5 ) ( x + 1 ) . Hàm số y = f ( x 2 ) đồng biến trên khoảng nào dưới đây?
A. (-2;-1).
B. (-2;0).
C. (0;1).
D. (-1;0).
Cho hàm số
y
f
(
x
)
,
hàm số
y
f
(
x
)
có đồ thị như hình vẽ dưới đây. Hỏi hàm số
y
f
x
2
−
1
đồng biến trên khoảng nào? A.
−
∞
;...
Đọc tiếp
Cho hàm số y = f ( x ) , hàm số y = f ' ( x ) có đồ thị như hình vẽ dưới đây. Hỏi hàm số y = f x 2 − 1 đồng biến trên khoảng nào?
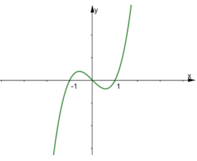
A. − ∞ ; − 2
B. (-1;1)
C. 1 ; 2
D. (0;1)
Cho hàm số yf(x) có đạo hàm trên và đồ thị hàm số yf’(x) như hình vẽ bên. Hàm số g(x)
2
f
1
-
x
+
1
3
x
3
-
4
x
-
1
đồng biến trên khoảng nào dưới đây? A.
-
∞
;
-
2...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên và đồ thị hàm số y=f’(x) như hình vẽ bên. Hàm số g(x) = 2 f 1 - x + 1 3 x 3 - 4 x - 1 đồng biến trên khoảng nào dưới đây?
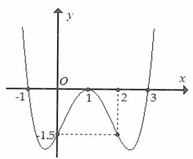
A. - ∞ ; - 2
B. (1;2)
C. 3 ; + ∞
D. (2;3)
Cho hàm số f(x) có
f
(
x
)
x
2
-
2
x
,
∀
x
∈
R
. Hàm số
y
f
(
1
-
x
2
)
+
4
x
đồng biến trên khoảng nào dưới đây ? A.
-
6
;...
Đọc tiếp
Cho hàm số f(x) có f ' ( x ) = x 2 - 2 x , ∀ x ∈ R . Hàm số y = f ( 1 - x 2 ) + 4 x đồng biến trên khoảng nào dưới đây ?
A. - 6 ; 6
B. - ∞ ; 6
C. - 6 2 ; 6 2
D. - 6 2 ; + ∞
Cho hàm số yf(x)có bảng xét dấu của đạo hàm như sauHàm số yf(1-2x) đồng biến trên khoảng nào dưới đây? A.
-
3
2
;
-
1
B.
-
∞
;
-
1
C. (-1;0) D.
-...
Đọc tiếp
Cho hàm số y=f(x)có bảng xét dấu của đạo hàm như sau

Hàm số y=f(1-2x) đồng biến trên khoảng nào dưới đây?
A. - 3 2 ; - 1
B. - ∞ ; - 1
C. (-1;0)
D. - ∞ ; - 2
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f’(x) và các khẳng định sau:(1). Hàm số yf(x) đồng biến trên khoảng
1
;
+
∞
(2). Hàm số yf(x) nghịch biến trên khoảng
-
∞
;
-
2
(3). Hàm số yf(x) nghịch biến trên khoảng
-...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Cho hàm số yf(x) có bảng xét dấu đạo hàm như sau Hàm số
y
f
(
3
x
+
1
)
-
x
3
+
3
x
đồng biến trên khoảng nào dưới đây? A.
3
4
;
1
B.
2...
Đọc tiếp
Cho hàm số y=f(x) có bảng xét dấu đạo hàm như sau

Hàm số y = f ( 3 x + 1 ) - x 3 + 3 x đồng biến trên khoảng nào dưới đây?
A. 3 4 ; 1
B. 2 3 ; 1
C. 1 4 ; 1 3
D. - 1 ; - 1 3
Hàm số yf(x) có đạo hàm
f
(
x
)
x
(
x
-
1
)
2
(
x
-
2
)
,
∀
x
∈
R
. Hàm số yf(x) nghịch biến trên khoảng nào dưới đây ? A.
(
2
;
+
∞
)
. B. (0;2). C.
(
-
∞
;
0...
Đọc tiếp
Hàm số y=f(x) có đạo hàm f ' ( x ) = x ( x - 1 ) 2 ( x - 2 ) , ∀ x ∈ R . Hàm số y=f(x) nghịch biến trên khoảng nào dưới đây ?
A. ( 2 ; + ∞ ) .
B. (0;2).
C. ( - ∞ ; 0 ) .
D. ( 1 ; + ∞ ) .



