Chọn B.
Ta có:
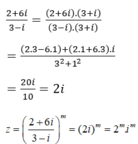
z là số thuần ảo khi và chỉ khi
![]()
![]()
Chọn B.
Ta có:
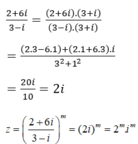
z là số thuần ảo khi và chỉ khi
![]()
![]()
Cho số phức z = 2 + 6 i 3 - i m m nguyên dương. Có bao nhiêu giá trị 1≤ m≤ 50 để z là số thuần ảo?
A. 26.
B. 25.
C. 24.
D. 50.
Cho số phức z = 4 i i + 1 m , m nguyên dương. Có bao nhiêu giá trị m ∈ [1;100] để z là số thực?
A. 27.
B. 26.
C. 25.
D. 28.
Có bao nhiêu giá trị nguyên của m để có đúng 2 số phức z thỏa mãn z - ( m - 1 ) + i = 8 và z - 1 + i = z - 2 + 3 i .
A. 130
B. 66
C. 65
D. 131
Có bao nhiêu số phức z thỏa mãn các điều kiện z - 2 + i = 2 v à ( z + i ) 2 là số thuần ảo?
![]()
![]()
![]()
![]()
Có bao nhiêu số phức z thỏa mãn z - i = 2 ; z 2 là số thuần ảo?
![]()
![]()
![]()
![]()
Tìm giá trị của số thực m sao cho số phức z = 2 - i 1 + m i là một số thuần ảo
A. Không tồn tại m.
B. m = - 1 2
C. m = -2
D. m = 2
Có bao nhiêu số phức z thỏa mãn: z - i = 2 và z 2 là số thuần ảo
A. 3
B. 1
C. 4
D. 2
Có bao nhiêu số phức z thỏa mãn z - i = 2 v à z 2 là số thuần ảo
![]()
![]()
![]()
![]()
Có bao nhiêu số phức z thỏa mãn z + 1 - 2 i = z ¯ + 3 + 4 i và z - 2 i z + i ¯ là một số thuần ảo
![]()
![]()
![]()
![]()