Một lò xo nhẹ có k 100/m treo thẳng đứng, đầu dưới treo hai vật nặng m 1 = m 2 = 100 g . Khoảng cách từ m2 tới mặt đất là h = 4 , 9 18 m . Bỏ qua khoảng cách hai vật. Khi hệ đang đứng yên ta đốt dây nối hai vật. Hỏi khi vật m2 chạm đất thì m1 đã đi được quãng đường bằng bao nhiêu?

A. s = 4,5 cm.
B. s = 3,5cm
C. s = 3,25 cm.
D. s = 4,25cm
+ Vật m1 sẽ dao động điều hòa quanh vị tíí cân bằng mới (ở trên vị trí cân bằng cũ 1 đoạn 0,5Δℓ) với biên độ A = 0 , 5 Δ ℓ 0 = 1 c m .
Chu kì của dao động T = 2 π m k = 0 , 2 s
+ Vật m2 sẽ rơi tự do với thời gian rơi là Δ t = 2 h g = 7 20 s
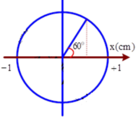
+ Tại thời điểm đốt dây (t = 0), m1 đang ở biên. Khoảng cách thời gian Δt tương ứng với góc quét
Δ φ = 7 π 3 = 2 π + π 3
→ Từ hình vẽ: S = 4 A + 0 , 5 A = 4 , 5 c m
Chọn đáp án A