Giải thích :Tỉ trọng sản lượng lương thực và số dân của nước ta so với thế giới năm 2014 lần lượt là 8,1% và 2,1%. Nước ta là một trong những nước có sản lượng lương thực luôn đứng vào top đầu của thế giới và xuất khẩu lúa gạo đứng top 5 của thế giới
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho bảng số liệu SẢN LƯỢNG LƯƠNG THỰC VÀ SỐ DÂN CỦA MỘT SỐ NƯỚC TRÊN THẾ GIỚI NĂM 2014 Để thể hiện sản lượng lương thực và số dân của một số nước trên thế giới năm 2014, biểu đồ thích hợp nhất là A. Biểu đồ cột. B. Biểu đồ tròn. C. Biểu đồ miền. D. Biểu đồ đường.
Đọc tiếp
Cho bảng số liệu
SẢN LƯỢNG LƯƠNG THỰC VÀ SỐ DÂN CỦA MỘT SỐ NƯỚC TRÊN THẾ GIỚI NĂM 2014
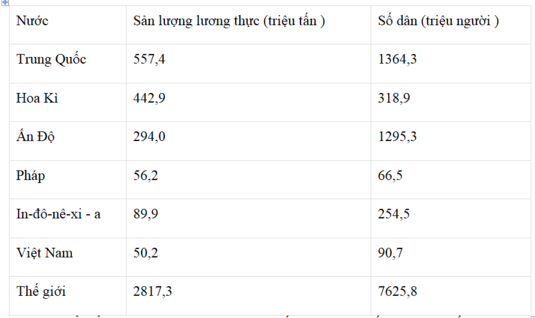
Để thể hiện sản lượng lương thực và số dân của một số nước trên thế giới năm 2014, biểu đồ thích hợp nhất là
A. Biểu đồ cột.
B. Biểu đồ tròn.
C. Biểu đồ miền.
D. Biểu đồ đường.
Cho bảng số liệu: Sản lượng lương thực và dân số của một số nước trên thế giới, năm 2002.Để thể hiện sản lượng lương thực và dân số của một số nước trên thế giới năm theo bảng số liệu, biểu đồ nào sau đây là thích hợp nhất? A. Tròn. B. Miền C. Cột ghép. D. Đường.
Đọc tiếp
Cho bảng số liệu: Sản lượng lương thực và dân số của một số nước trên thế giới, năm 2002.
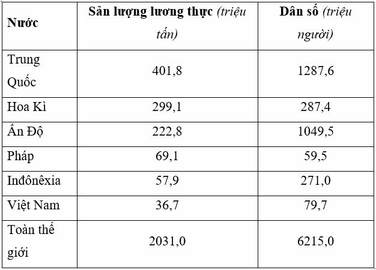
Để thể hiện sản lượng lương thực và dân số của một số nước trên thế giới năm theo bảng số liệu, biểu đồ nào sau đây là thích hợp nhất?
A. Tròn.
B. Miền
C. Cột ghép.
D. Đường.
Cho bảng số liệu:Sản lượng lương thực và dân số của một số nước trên thế giới năm 2002Để thể hiện sản lượng lương thực và dân số của một số nước trên thế giới theo biểu đồ năm thời kì 1950 -2003, biểu đồ nào sau đây là thích hợp nhất? A. Tròn B. Miền C. Cột ghép D. Đường
Đọc tiếp
Cho bảng số liệu:
Sản lượng lương thực và dân số của một số nước trên thế giới năm 2002
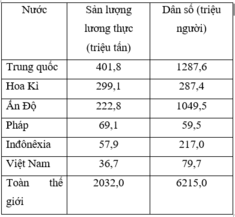
Để thể hiện sản lượng lương thực và dân số của một số nước trên thế giới theo biểu đồ năm thời kì 1950 -2003, biểu đồ nào sau đây là thích hợp nhất?
A. Tròn
B. Miền
C. Cột ghép
D. Đường
Giả sử tỉ suất gia tăng dân số của toàn thế giới năm 2015 là 1,2% và không thay đổi trong suốt thời kì 2000 – 2020 , biết rằng số dân toàn thế giới năm 2015 là 7346 triệu người . Số dân của năm 2014 là A. 7257,8 triệu người. B. 7287,8 triệu người. C. 7169,6 triệu người. D. 7258,9 triệu người.
Đọc tiếp
Giả sử tỉ suất gia tăng dân số của toàn thế giới năm 2015 là 1,2% và không thay đổi trong suốt thời kì 2000 – 2020 , biết rằng số dân toàn thế giới năm 2015 là 7346 triệu người . Số dân của năm 2014 là
A. 7257,8 triệu người.
B. 7287,8 triệu người.
C. 7169,6 triệu người.
D. 7258,9 triệu người.
Để thể hiện cơ cấu sản lượng thực và cơ cấu số dân của thế giới phân theo nước năm 2014, biểu đồ thích hợp nhất là
A. Biểu đồ cột.
B. Biểu đồ tròn
C. Biểu đồ miền.
D. Biểu đồ kết hợp ( cột, đường ).
Giả sử tỉ suất gia tăng dân số của toàn thế giới năm 2015 là 1,2% và không thay đổi trong suốt thời kì 2000 – 2020 , biết rằng số dân toàn thế giới năm 2015 là 7346 triệu người . Số dân của năm 2016 sẽ là A. 7468,25 triệu người. B. 7458,25 triệu người. C. 7434,15 triệu người. D. 7522,35 triệu người.
Đọc tiếp
Giả sử tỉ suất gia tăng dân số của toàn thế giới năm 2015 là 1,2% và không thay đổi trong suốt thời kì 2000 – 2020 , biết rằng số dân toàn thế giới năm 2015 là 7346 triệu người . Số dân của năm 2016 sẽ là
A. 7468,25 triệu người.
B. 7458,25 triệu người.
C. 7434,15 triệu người.
D. 7522,35 triệu người.
Cho bảng số liệu:Sản xuất lương thực thế giới thời kì 1980 – 2003(Đơn vị: triệu tấn)Để thể hiện quy mô và cơ cấu lương thực thế giới năm 1980, 1990, 2003 theo bảng số liệu, biểu đồ nào sau đây là thích hợp nhất? A. Đường. B. Tròn. C. Miền D. Cột chồng.
Đọc tiếp
Cho bảng số liệu:
Sản xuất lương thực thế giới thời kì 1980 – 2003
(Đơn vị: triệu tấn)
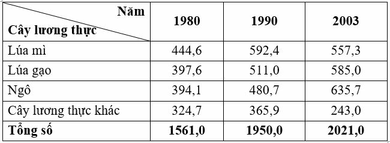
Để thể hiện quy mô và cơ cấu lương thực thế giới năm 1980, 1990, 2003 theo bảng số liệu, biểu đồ nào sau đây là thích hợp nhất?
A. Đường.
B. Tròn.
C. Miền
D. Cột chồng.
Để thể hiện bình quân lương thực theo đầu người của một số nước trên thế giới năm 2014, biểu đồ thích hợp nhất là
A. Biểu đồ cột.
B. Biểu đồ tròn.
C. Biểu đồ miền.
D. Biểu đồ kết hợp ( cột, đường ).
Để thể hiện bình quân lương thực theo đầu người của một số nước trên thế giới năm 2014, biểu đồ thích hợp nhất là
A. Biểu đồ cột.
B. Biểu đồ tròn.
C. Biểu đồ miền.
D. Biểu đồ kết hợp ( cột, đường ).



