Cho tam giác ABC cân tại A có A = 50 độ . Gọi M là trung điểm của BC. a) Tính số đo góc B, góc C, so sánh AB và BC b) Chứng minh ΔΑΒΜ = ΔАСМ. c) Chứng minh AM vuông góc với BC. d) Trên tia đối của tia AB lấy điểm E sao cho AE = AB Từ E vẽ đoạn thẳng vuông góc với tia MA tại D. Chứng minh : EC vuông góc với ED tại E.
Ôn tập Tam giác
a: Ta có: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-\widehat{BAC}}{2}=65^0\)
Xét ΔABC có \(\widehat{ACB}>\widehat{BAC}\)
mà AB,BC lần lượt là cạnh đối diện của các góc ACB,BAC
nên AB>BC
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
c: ta có: ΔABM=ΔACM
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, AB 5 cm. Tia phân giác góc B cắt Ac tại D. Từ D kẻ đường thẳng vuông góc với BC tại E. a) Chứng minh BE AB b) Chứng minh tam giác AEB là tam giác đều c) Tính BC d) Trên tia đối của tia AB lấy K sao cho AK EC. Chứng minh K, D, E thẳng hàng
Đọc tiếp
Cho tam giác ABC vuông tại A, AB = 5 cm. Tia phân giác góc B cắt Ac tại D. Từ D kẻ đường thẳng vuông góc với BC tại E.
a) Chứng minh BE =AB
b) Chứng minh tam giác AEB là tam giác đều
c) Tính BC
d) Trên tia đối của tia AB lấy K sao cho AK = EC. Chứng minh K, D, E thẳng hàng
Em ghi thiếu đề rồi, đề phải có thêm 1 dữ kiện về độ dài cạnh AC hoặc góc B, góc C
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Lấy M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA. Chứng minh rằng a) tam giác ABC= tam giác CDA b) AM=½BC
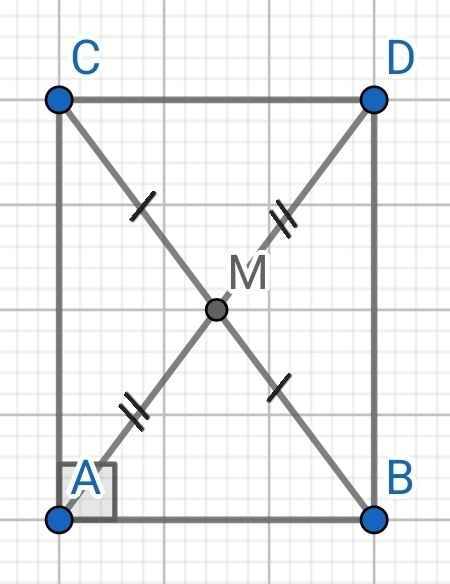
a) Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆AMB và ∆DMC có:
AM = DM (gt)
∠AMB = ∠DMC (đối đỉnh)
MB = MC (cmt)
⇒ ∆AMB = ∆DMC (c-g-c)
⇒ ∠MAB = ∠MDC (hai góc tương ứng)
Lại có:
∠MAC + ∠MAB = 90⁰ (∆ABC vuông tại A)
⇒ ∠MAC + ∠MDC = 90⁰
⇒ ∠DAC + ∠ADC = 90⁰
∆CDA có:
∠DAC + ∠CDA + ∠ACD = 180⁰ (tổng ba góc trong ∆ACD)
⇒ ∠ACD = 180⁰ - (∠DAC + ∠CDA)
= 180⁰ - 90⁰
= 90⁰
⇒ ∆ACD vuông tại C
Do ∆AMB = ∆DMC (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ABC và ∆CDA có:
AC là cạnh chung
AB = CD (cmt)
⇒ ∆ABC = ∆CDA (hai cạnh góc vuông)
b) Do ∆ABC = ∆CDA (cmt)
⇒ BC = AD (hai cạnh tương ứng)
Do AM = DM (gt)
⇒ AM = DM = ½AD
Mà AD = BC (cmt)
⇒ AM = ½BC
Đúng 1
Bình luận (0)
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
DO đó: ABDC là hình bình hành
Suy ra: AB=DC; AC=BD
Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
Do đó: ΔABC=ΔCDA
b: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=1/2BC
Đúng 2
Bình luận (0)
Cho tam giác MNP có góc m bằng 140 độ các đường trung trực của MN và MP lần lượt cắt NP ở E và F tính góc em EMF
E nằm trên đường trung trực của MN
=>EM=EN
=>ΔEMN cân tại E
=>\(\widehat{EMN}=\widehat{ENM}\)
F nằm trên đường trung trực của MP
=>FM=FP
=>ΔFMP cân tại F
=>\(\widehat{FMP}=\widehat{FPM}\)
Ta có: \(\widehat{EMN}+\widehat{FMP}=\widehat{N}+\widehat{P}\)
\(=180^0-\widehat{NMP}=40^0\)
Ta có: \(\widehat{EMN}+\widehat{FMP}+\widehat{EMF}=\widehat{NMP}\)
=>\(\widehat{EMF}+40^0=140^0\)
=>\(\widehat{EMF}=100^0\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A các tia phân giác của góc B và góc C cắt nhau tại I gọi H J K LẦN LƯỢT LÀ CHÂN ĐƯỜNG VUÔNG GÓC KẺ TỪ 1 ĐẾN AB AC BC biết kI bằng 5 cm và BK = 10 cm và KC = 15 cm tính diện tích tam giác ABC
Cho tam giác nhọn AMN VẼ AH VUÔNG GÓC VỚI MN GỌI O LÀ MỘT ĐIỂM NẰM TRÊN ĐOẠN THẲNG AH BIẾT CHU VI TAM GIÁC AMN LÀ 38 VÀ MN = 8 TÌM GIÁ TRỊ LỚN NHẤT CỦA TỔNG OM + ON GIÚP VỚI PLS
Cho tam giác MNP cân tại P với góc P nhỏ hơn 90 độ và A là trung điểm của M N CÂU A CHỨNG MINH TAM GIÁC NAP BẰNG TAM GIÁC MAP VÀ PA VUÔNG GÓC VỚI MN câu b gọi B là trung điểm của PN và MB cắt PA Tại G . Tính AB và GB biết MP bằng 13 cm và MN = 10 cm câu c trên tia đối của tia BM LẤY ĐIỂM C SAO CHO BG = BC CHỨNG MINH CM LỚN HƠN CN GIÚP VỚI PLS
a: Xét ΔPAM và ΔPAN có
PA chung
AM=AN
PM=PN
Do đó: ΔPAM=ΔPAN
=>\(\widehat{PAM}=\widehat{PAN}\)
mà \(\widehat{PAM}+\widehat{PAN}=180^0\)
nên \(\widehat{PAM}=\widehat{PAN}=\dfrac{180^0}{2}=90^0\)
=>PA\(\perp\)MN
b: ta có: A là trung điểm của MN
=>\(MA=AN=\dfrac{MN}{2}=5\left(cm\right)\)
Xét ΔPAM vuông tại A có \(PA^2+AM^2=PM^2\)
=>\(PA^2=13^2-5^2=144=12^2\)
=>PA=12(cm)
Xét ΔNMP có
A,B lần lượt là trung điểm của NM,NP
=>AB là đường trung bình của ΔNMP
=>\(AB=\dfrac{MP}{2}=6,5\left(cm\right)\)
Đúng 2
Bình luận (1)
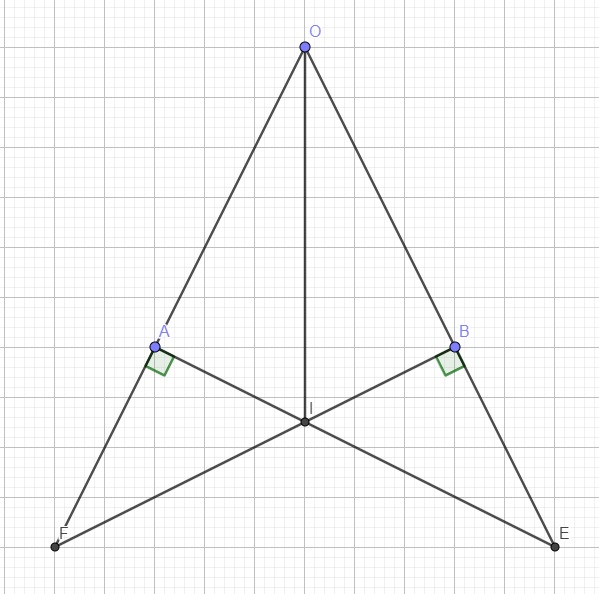
Cho góc nhọn xOy.Trên Ox,Oy lần lượt lấy 2 điểm A,B sao cho OA=OB.Từ A kẻ đường thẳng vuông góc với Ox cắt Oy tại E.Từ B kẻ đường thẳng vuông góc với Ox cắt Ox tại F.AE và BF cắt nhau tại I
Chứng minh:
a,AE=BF
b,tam giác AFI=tam giác BEI
c,OI là phân giác của AOB
Mong các bạn chữa bài này của mình nhé.
a.
Do \(BF\perp OE\left(gt\right)\Rightarrow\widehat{OBF}=90^0\)
Do \(AE\perp OF\Rightarrow\widehat{OAE}=90^0\)
Xét hai tam giác OAE và OBF có:
\(\left\{{}\begin{matrix}\widehat{O}-chung\\OA=OB\left(gt\right)\\\widehat{OAE}=\widehat{OBF}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta OAE=\Delta OBF\left(g.c.g\right)\)
\(\Rightarrow AE=BF\)
b.
Từ câu a, do \(\Delta OAE=\Delta OBF\Rightarrow OE=OF\)
\(\Rightarrow OB+BE=OA+AF\)
Mà \(OA=OB\Rightarrow BE=AF\)
Lại có \(\widehat{AIF}=\widehat{BIE}\) (hai góc đối đỉnh)
\(\Rightarrow90^0-\widehat{AFI}=90^0-\widehat{BEI}\) (các tam giác AFI và BEI vuông)
\(\Rightarrow\widehat{AFI}=\widehat{BEI}\)
Xét hai tam giác AFI và BEI có:
\(\left\{{}\begin{matrix}\widehat{AFI}=\widehat{BEI}\left(cmt\right)\\AF=BE\left(cmt\right)\\\widehat{IAF}=\widehat{IBE}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AFI=\Delta BEI\left(g.c.g\right)\)
c.
Từ câu b, do \(\Delta AFI=\Delta BEI\Rightarrow AI=BI\)
Xét hai tam giác OAI và OBI có:
\(\left\{{}\begin{matrix}OA=OB\left(gt\right)\\OI-chung\\AI=BI\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta OAI=\Delta OBI\left(c.c.c\right)\)
\(\Rightarrow\widehat{AOI}=\widehat{BOI}\)
\(\Rightarrow OI\) là phân giác góc \(\widehat{AOB}\)
Đúng 1
Bình luận (0)
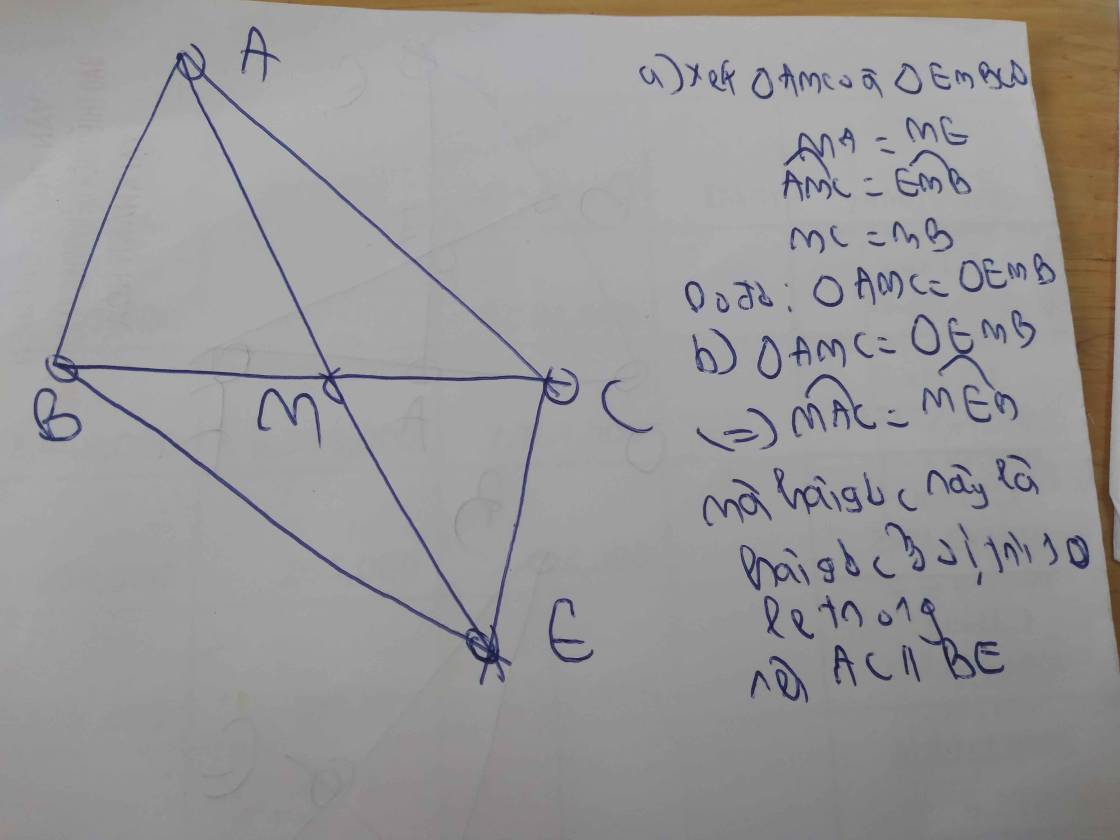
Cho tam giác ABC,M là trung điểm của BC.Trên tia AM lấy điểm E sao cho AM=ME
a)Chứng minh tam giác AMC=tam giác EMB
b)Chứng minh AC song song với BE
(Trả lời và vẽ hình giúp mik với ạ ! Mình xin chân thành cảm ơn)
Cho tam giác ABC có góc ABC =35°; góc ACB =65° a, Tính số đo góc BAC b, Tìm cạnh lớn nhất và bé nhất của tam giác ABC c, Vẽ AI vuông góc với BC ( I thuộc cạnh BC ). Trên đoạn AI lấy điểm D, trên đoạn IB lấy điểm E. Chứng minh DE < AB
a: Xét ΔABC có
\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{BAC}+35^0+65^0=180^0\)
=>\(\widehat{BAC}=80^0\)
b: Xét ΔABC có \(\widehat{BAC}>\widehat{ACB}>\widehat{ABC}\)
mà BC,AB,AC lần lượt là cạnh đối diện của các góc BAC;ACB;ABC
nên BC>AB>AC
=>Cạnh lớn nhất là BC, cạnh nhỏ nhất là AC
c: Xét ΔIDE có \(\widehat{ADE}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADE}=\widehat{DIE}+\widehat{DEI}=90^0+\widehat{DEI}>90^0\)
Xét ΔADE có \(\widehat{ADE}>90^0\)
nên AE là cạnh lớn nhất
=>AE>DE
Xét ΔAIE có \(\widehat{AEB}\) là góc ngoài tại đỉnh E
nên \(\widehat{AEB}=\widehat{EIA}+\widehat{EAI}=90^0+\widehat{EAI}>90^0\)
Xét ΔAEB có \(\widehat{AEB}>90^0\)
nên AB là cạnh lớn nhất trong ΔAEB
=>AB>AE
mà AE>DE
nên DE<AB
Đúng 0
Bình luận (0)