
Ôn tập: Tam giác đồng dạng
Hải đăng Đá Lát là một trong bảy ngọn hải đăng cao nhất Việt Nam được đặt trên đảo Đá Lát ở vị trí cực Tây quần đảo thuộc xã đảo Trường Sa, huyện Trường Sa, tỉnh Khánh Hòa. Ngọn hải đăng được xây dựng năm 1994 cao 42m, có tác dụng chỉ vị trí đảo, giúp quan sát tàu thuyền hoạt động trong vùng biển Trường Sa, định hướng và xác định vị trí của mình. Một người cao 1,65m đang đứng trên ngọn hải đăng quan sát hai lần một chiếc tàu. Lần thứ nhất người đó nhìn thấy chiếc tàu với góc hạ30độ, lần thứ hai...
Đọc tiếp
Hải đăng Đá Lát là một trong bảy ngọn hải đăng cao nhất Việt Nam được đặt trên đảo Đá Lát ở vị trí cực Tây quần đảo thuộc xã đảo Trường Sa, huyện Trường Sa, tỉnh Khánh Hòa. Ngọn hải đăng được xây dựng năm 1994 cao 42m, có tác dụng chỉ vị trí đảo, giúp quan sát tàu thuyền hoạt động trong vùng biển Trường Sa, định hướng và xác định vị trí của mình. Một người cao 1,65m đang đứng trên ngọn hải đăng quan sát hai lần một chiếc tàu. Lần thứ nhất người đó nhìn thấy chiếc tàu với góc hạ30độ, lần thứ hai người đó nhìn thấy chiếc tàu với góc hạ 60độ. Biết hai vị trí được quan sát của tàu và chân hải đăng là 3 điểm thẳng hàng. Hỏi sau hai lần quan sát, tàu đã chạy được bao nhiêu mét?
Cho ∆ABC vuông tại A. Kẻ đường cao AH. Đường phân giác của góc ABC cắt AC tại D và cắt AH tại E. a) Biết AB 9cm, BC 15cm. Tính AC? b) Chứng minh: ∆ABC ∆HBA c) Gọi I là trung điểm của ED. Chứng minh EI/EA EH/EBd). Chứng minh: góc BIH góc ACB
Đọc tiếp
Cho ∆ABC vuông tại A. Kẻ đường cao AH. Đường phân giác của góc ABC cắt AC tại D và cắt AH tại E.
a) Biết AB = 9cm, BC = 15cm. Tính AC?
b) Chứng minh: ∆ABC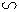 ∆HBA c) Gọi I là trung điểm của ED. Chứng minh EI/EA = EH/EB
∆HBA c) Gọi I là trung điểm của ED. Chứng minh EI/EA = EH/EB
d). Chứng minh: góc BIH = góc ACB
a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=15^2-9^2=144=12^2\)
=>AC=12(cm)
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
c: Ta có: \(\widehat{HEB}+\widehat{HBE}=90^0\)(ΔHBE vuông tại H)
\(\widehat{ABD}+\widehat{ADE}=90^0\)(ΔABD vuông tại A)
mà \(\widehat{HBE}=\widehat{ABD}\)
nên \(\widehat{HEB}=\widehat{ADE}\)
mà \(\widehat{HEB}=\widehat{AED}\)(hai góc đối đỉnh)
nên \(\widehat{ADE}=\widehat{AED}\)
=>ΔADE cân tại A
Ta có: ΔADE cân tại A
mà AI là đường trung tuyến
nên AI\(\perp\)DE
Xét ΔEIA vuông tại I và ΔEHB vuông tại H có
\(\widehat{AEI}=\widehat{BEH}\)(hai góc đối đỉnh)
Do đó: ΔEIA~ΔEHB
=>\(\dfrac{EI}{EH}=\dfrac{EA}{EB}\)
=>\(\dfrac{EI}{EA}=\dfrac{EH}{EB}\)
d: Xét tứ giác AIHB có \(\widehat{AIB}=\widehat{AHB}=90^0\)
nên AIHB là tứ giác nội tiếp
=>\(\widehat{BIH}=\widehat{BAH}\)
mà \(\widehat{BAH}=\widehat{C}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{BIH}=\widehat{C}\)
Đúng 1
Bình luận (0)
cho hình bình hành vuông ABCD, góc A= góc D=90 độ AB=4cm CD=9cm AD=6cm
1)tam giác BAD đồng dạng với tam giác ADC
2) AC vuông góc với BD
3) gọi O là giao điểm của AC và BD tính tỉ số diện tích ADB/COD
4)gọi K là giao điểm của DA và CB tính độ dài KA
cứu em hôm nay với
1: Sửa đề: Hình thang vuông ABCD
Xét ΔBAD vuông tại A và ΔADC vuông tại D có
\(\dfrac{BA}{AD}=\dfrac{AD}{DC}\left(\dfrac{4}{6}=\dfrac{6}{9}=\dfrac{2}{3}\right)\)
Do đó: ΔBAD~ΔADC
2: Ta có: ΔBAD~ΔADC
=>\(\widehat{ABD}=\widehat{DAC}\)
mà \(\widehat{ABD}+\widehat{ADB}=90^0\)(ΔABD vuông tại A)
nên \(\widehat{DAC}+\widehat{ADB}=90^0\)
=>AC\(\perp\)DB
4: Xét ΔKDC có AB//DC
nên \(\dfrac{AB}{DC}=\dfrac{KA}{KD}\)
=>\(\dfrac{KA}{KA+6}=\dfrac{4}{9}\)
=>\(9KA=4\left(KA+6\right)\)
=>\(9\cdot KA=4\cdot KA+24\)
=>5*KA=24
=>KA=24/5=4,8(cm)
Đúng 1
Bình luận (1)
Cho tam giác nhọn ABC có đường cao là AD, lấy điểm H trên đoạn AD sao cho BD.CD =DH.DA. a) Chứng minh: H là trực tâm của tam giác ABC . b) Dựng các đường cao BE,CF . Gọi I là giao điểm của EF với AH ,K là trung điểm AH . Chứng minh I là trực tâm tam giác KBC . c) Trên đoạn BH ,CH lần lượt lấy các điểm Q,R sao cho AQC =ARB = 900 . Chứng minh: AQ =AR .
a: \(BD\cdot CD=DH\cdot DA\)
=>\(\dfrac{BD}{DH}=\dfrac{DA}{CD}\)
Xét ΔBDA vuông tại D và ΔHDC vuông tại D có
\(\dfrac{BD}{HD}=\dfrac{DA}{DC}\)
Do đó: ΔBDA~ΔHDC
=>\(\widehat{DBA}=\widehat{DHC}\)
mà \(\widehat{DHC}+\widehat{DCH}=90^0\)
nên \(\widehat{DCH}+\widehat{DBA}=90^0\)
=>CH\(\perp\)AB
Xét ΔABC có
CH,AD là các đường cao
CH cắt AD tại H
Do đó: H là trực tâm của ΔABC
c: Xét ΔAQC vuông tại Q có QE là đường cao
nên \(AE\cdot AC=AQ^2\left(1\right)\)
Xét ΔARB vuông tại R có RF là đường cao
nên \(AF\cdot AB=AR^2\left(2\right)\)
Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB~ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(AE\cdot AC=AB\cdot AF\left(3\right)\)
Từ (1),(2),(3) suy ra AQ=AR
Đúng 2
Bình luận (1)
 ccứu
ccứu
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{ACB}\) chung
Do đó: ΔABC~ΔHAC
b:
Ta có: HM là phân giác của góc AHB
=>\(\widehat{AHM}=\widehat{BHM}=\dfrac{\widehat{AHB}}{2}=45^0\)
ta có: HN là phân giác của góc AHC
=>\(\widehat{AHN}=\widehat{CHN}=\dfrac{\widehat{AHC}}{2}=45^0\)
Xét ΔMAH và ΔNCH có
\(\widehat{MHA}=\widehat{NHC}\left(=45^0\right)\)
\(\widehat{MAH}=\widehat{NCH}\left(=90^0-\widehat{ABH}\right)\)
Do đó: ΔMAH~ΔNCH
c: Ta có: ΔMAH~ΔNCH
=>\(\dfrac{HM}{HN}=\dfrac{HA}{HC}\)
Ta có; ΔABC~ΔHAC
=>\(\dfrac{HA}{AB}=\dfrac{HC}{AC}\)
=>\(\dfrac{HA}{HC}=\dfrac{AB}{AC}\)
=>\(\dfrac{HM}{HN}=\dfrac{AB}{AC}\)
=>\(\dfrac{HM}{AB}=\dfrac{HN}{AC}\)
\(\widehat{MHN}=\widehat{MHA}+\widehat{NHA}=90^0\)
Xét ΔHMN vuông tại H và ΔABC vuông tại A có
\(\dfrac{HM}{AB}=\dfrac{HN}{AC}\)
Do đó: ΔHMN~ΔABC
d: Xét tứ giác AMHN có \(\widehat{NAM}+\widehat{NHM}=90^0+90^0=180^0\)
nên AMHN là tứ giác nội tiếp
=>\(\widehat{AMN}=\widehat{AHN}=45^0\)
Xét ΔAMN vuông tại A có \(\widehat{AMN}=45^0\)
nên ΔAMN vuông cân tại A
Đúng 1
Bình luận (0)
 chi tiêt
chi tiêt
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
Xét ΔHCA vuông tại H và ΔACB vuông tại A có
\(\widehat{HCA}\) chung
Do đó: ΔHCA~ΔACB
Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó; ΔHAB~ΔHCA
b:
1: Ta có: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BH\cdot BC\)
2: Ta có: ΔCHA~ΔCAB
=>\(\dfrac{CH}{CA}=\dfrac{CA}{CB}\)
=>\(CH\cdot CB=CA^2\)
3: Ta có: ΔHBA~ΔHAC
=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)
=>\(HA^2=BH\cdot HC\)(1)
c: Xét ΔAEH vuông tại E và ΔAHB vuông tại H có
\(\widehat{HAE}\) chung
Do đó: ΔAHE~ΔABH
=>\(\dfrac{AH}{AB}=\dfrac{AE}{AH}\)
=>\(AH^2=AB\cdot AE\left(2\right)\)
Xét ΔAKH vuông tại F và ΔAHC vuông tại H có
\(\widehat{KAH}\) chung
Do đó: ΔAKH~ΔAHC
=>\(\dfrac{AK}{AH}=\dfrac{AH}{AC}\)
=>\(AH^2=AK\cdot AC\left(3\right)\)
Từ (1),(2),(3) suy ra \(AH^2=AE\cdot AB=AK\cdot AC\)
d: Ta có: \(AE\cdot AB=AK\cdot AC\)
=>\(\dfrac{AE}{AC}=\dfrac{AK}{AB}\)
Xét ΔAEK vuông tại E và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AK}{AB}\)
Do đó: ΔAEK~ΔACB
Đúng 1
Bình luận (0)
 cchitieest
cchitieest
a: Xét ΔCMF vuông tại M và ΔCAB vuông tại A có
\(\widehat{MCF}\) chung
Do đó: ΔCMF~ΔCAB
b: Xét ΔBME vuông tại M và ΔBAC vuông tại A có
\(\widehat{MBE}\) chung
Do đó: ΔBME~ΔBAC
=>\(\dfrac{BM}{BA}=\dfrac{BE}{BC}\)
=>\(BM\cdot BC=BA\cdot BE\)
c: Xét ΔBCF có
BA,FM là các đường cao
BA cắt FM tại E
Do đó: E là trực tâm của ΔBCF
=>CE\(\perp\)BF tại K
Xét ΔCME vuông tại M và ΔCKB vuông tại K có
\(\widehat{MCE}\) chung
Do đó: ΔCME~ΔCKB
=>\(\dfrac{CM}{CK}=\dfrac{CE}{CB}\)
=>\(CM\cdot CB=CK\cdot CE\)
\(BE\cdot BA+CE\cdot CK\)
\(=BM\cdot BC+CM\cdot CB\)
=BC(BM+CM)
=BC2 không phụ thuộc vào vị trí điểm M
Đúng 1
Bình luận (1)
 cứu làm bài 6 làm b7 càng tốt ạ
cứu làm bài 6 làm b7 càng tốt ạ
 cứu cHI tiết
cứu cHI tiết













