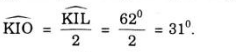Cho tam giác ABC vuông tại A .I là điểm nằm trong tam giác và cắt đều 3 cạnh của tam giác mọi khoảng cách từ I đến các cạnh của tam giác ABC là r . CMR : AB+AC-BC=2r
Bài 6: Tính chất ba đường phân giác của tam giác
Bạn ơi giúp mình câu này nhanh nhé mình cần gấp lắm![]() :
:
Cho tam giác ABC cân tại A,2tia phân giác góc A và B cắt nhau ở I.Kẻ AH vuông góc với AC,IN vuông góc với AC.Chứng minh rằng:
a)IA nhỏ hơn AM +AN
b)Cho BC=5cm;Ab=3cm.Tính AN
Đúng 0
Bình luận (1)
Cho Delta ABC nhọn , đường cao AH. Vẽ HM, HN lần lượt vuông góc với AB, AC. Trên tia đối của tia MH lấy điểm D sao cho MDMH.Trên tia đối của tia NH lấy điểm E sao cho NDNH. Gọi I và K là giao điểm của DE và AB, AB và AC. CMR:
a, IB là tia phân giác của widehat{HIB}
b,HA là tia phân giác của widehat{IHK}
c,IC là tia phân giác củawidehat{HIK}
d,IBperpIC
Đọc tiếp
Cho \(\Delta ABC\) nhọn , đường cao AH. Vẽ HM, HN lần lượt vuông góc với AB, AC. Trên tia đối của tia MH lấy điểm D sao cho MD=MH.Trên tia đối của tia NH lấy điểm E sao cho ND=NH. Gọi I và K là giao điểm của DE và AB, AB và AC. CMR:
a, IB là tia phân giác của \(\widehat{HIB}\)
b,HA là tia phân giác của \(\widehat{IHK}\)
c,IC là tia phân giác của\(\widehat{HIK}\)
d,IB\(\perp\)IC
B A F C D E chứng minh EA ED
Đọc tiếp
chứng minh EA= ED
_Xét 2 tam giác vuông BAE và BDE Ta có:
\(\)góc BAE=góc BDE=90 độ
BE: Cạnh huyền chung
\(\Rightarrow\)Tam giác BAE=tam giác BDE( Cạnh huyền-góc vuông)
\(\Rightarrow\)AE=ED( cặp cạnh thương ứng)
Đúng 0
Bình luận (1)
CHO TAM GIÁC ABC VUÔNG TẠI A .TIA PHÂN GIÁC GÓC C CẮT AB TẠI D .KẺ DH VUÔNG GÓC BC (H THUỘC BC).ĐƯỜNG THẲNG DH CẮT ĐƯỜNG THẲNG AC TẠI K
CM
a,CA=CH
b,TAM GIÁC AKD= TAM GIÁC HBD
c,AD<DB
Bn tự vẽ hình nhé
a) Xét tam giác ACD và tam giác HCD có :
\(\widehat{CAD}=\widehat{CHD}=90^0\)
CD : cạnh chung
\(\widehat{ACD}=\widehat{HCD}\) ( Vì CD là tia p/g \(\widehat{ACB}\))
\(\Rightarrow\Delta ACD=\Delta HCD\) ( cạnh huyền - góc nhọn)
=> CA = CH ( 2.c.t.ư)
Đúng 0
Bình luận (1)
b) Xét \(\Delta ADK\) và \(\Delta HDB\) có :
\(\widehat{DAK}=\widehat{DHB}=90^0\)
\(AD=DH\) (vì \(\Delta ADH=\Delta CDH\))
\(\widehat{ADK}=\widehat{HDB}\) ( 2 góc đối đỉnh)
=> \(\Delta ADK=\Delta HBD\left(g-c-g\right)\)
Đúng 0
Bình luận (0)
c) Xét \(\Delta HDB\) vuông tại H có :
\(DB>HD\) ( cạnh huyền lớn hơn cạnh góc vuông)
Ta có : \(\Delta AKD=\Delta HBD\) ( cm ở câu b)
\(\Rightarrow HD=AD\left(2.c.t.ư\right)\)
Mà \(DB>HD\) => DB>AD
Đúng 0
Bình luận (1)
Nêu công thức xác định đường phân giác trong tam giác
Không hiểu đề lắm.
Cách 1:
Đường thẳng nằm trong góc chia góc thành 2 phần bằng nhau.
Cách 2:
Điểm nằm trong góc sao cho cách đều 2 cạnh của góc.
Chúc bạn học tốt!!!
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, D là trung điểm của BC. Gọi E và F là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh DE = DF
Hình ảnh chỉ mang t/c minh họa
Do ΔABC cân tại A nên
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\) hay \(\widehat{EBD}=\widehat{FCD}\)
Xét ΔBDE và ΔCDF có :
\(\widehat{DEB}=\widehat{DFC}=90^o\)
\(\widehat{EBD}=\widehat{FCD}\left(cmt\right)\)
BD = CD ( D là trung điểm của BC )
=> ΔBDE = ΔCDF ( c.h-g.n )
=> DE = DF ( 2 cạnh tương ứng )
Đúng 0
Bình luận (0)
Cho tam giác ABC về phía ngoài tam giác, ta dựng các tam giác đều ABD, ACE, BCF. CHứn minh rằng 3 đường thẳng AF, BE, CD đồng quy
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm D sao cho widehat{ABC3.widehat{ABD}} trên cạnh AB lấy điểm E sao cho widehat{ACB}3.widehat{ACE} Gọi F là giao điểm của BD và CE. I là giao điểm của các tia phân giác của Delta BFC
a, Tính widehat{BFC}
b, Chứng minh rằng : Tam giác DEI là tam giác đều
Đọc tiếp
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm D sao cho \(\widehat{ABC=3.\widehat{ABD}}\) trên cạnh AB lấy điểm E sao cho \(\widehat{ACB}=3.\widehat{ACE}\) Gọi F là giao điểm của BD và CE. I là giao điểm của các tia phân giác của \(\Delta BFC\)
a, Tính \(\widehat{BFC}\)
b, Chứng minh rằng : Tam giác DEI là tam giác đều
a, Ta có \(\widehat{B}\) +\(\widehat{C}\) = 90
\(\Rightarrow\) \(\dfrac{2}{3}\)\(\widehat{B}\) +\(\dfrac{2}{3}\)\(\widehat{C}\)= 60
Xét tam giác CFB
\(\Rightarrow\) \(\widehat{CFB}\)= 180-60=120
Đúng 0
Bình luận (0)
Cho \(\Delta ABC;\widehat{A}=90^0\) trung tuyến \(AM\), Trên tia đối của MA lấy điểm D sao cho MD = MA. Qua D kẻ \(xy\perp BC\) Trên Ox lấy điểm P trên tia Oy lấy điểm Q sao cho DP = DQ = BC. CMR : AP, AQ là phân giác phân giác trong ngoài \(\widehat{BAC}\) của \(\Delta ABC\)
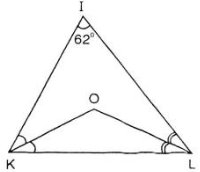
Cho hình 38 (SGK Toán 7 tập 2 trang 73)
a) Tính góc KOL.
b) Kẻ tia IO, hãy tính góc KIO.
c) Điểm O có cách đều ba cạnh của tam giác IKL không? Tại sao?
d) Tia phân giác của góc ngoài ΔIKL tại đỉnh L cắt KO tại E. Tính góc KEL ?
(Giúp mình nhé! Mình dang cần gấp câu d)b) ΔKIL có O là giao điểm của hai đường phân giác KO và LO nên OI là đường phân giác của góc KIL (định lí ba đường phân giác cùng đi qua một điểm).
Do đó:
c) Điểm O có cách đều 3 cạnh của tam giác IKL bởi vì O là giao điểm của ba đường phân giác trong tam giác đó.
Đúng 0
Bình luận (2)