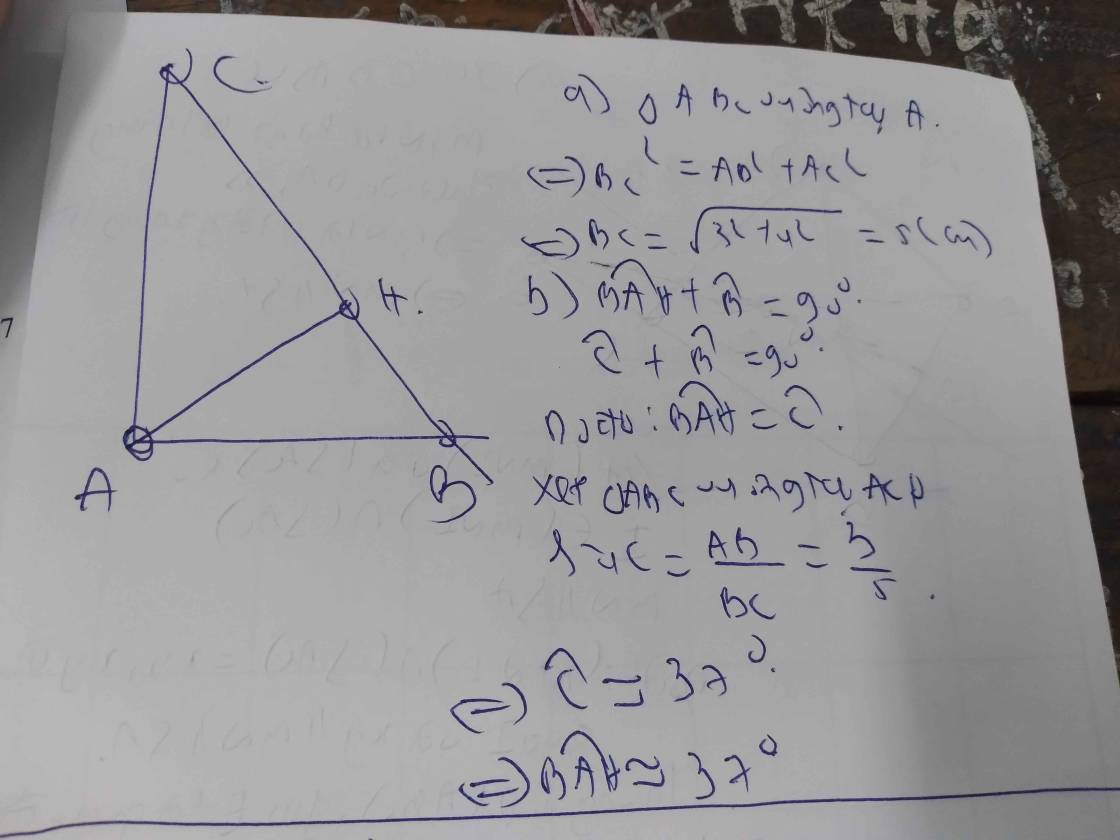
cho tam giác ABC vuông tại A, đường cáo AH, AC = 3 cm, HC = 1,8cm. Tính độ dài phân giác AD của tam giác ABC
Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông
Xét ΔABC vuông tại A có AH là đường cao
nên AC^2=CH*CB
=>CB=3^2/1,8=5cm
AB=căn 5^2-3^2=4cm
Xét ΔABC có AD là phân giác
nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{90}{2}\right)\)
\(=\dfrac{2\cdot3\cdot4}{3+4}\cdot cos45=\dfrac{12\sqrt{2}}{7}\left(cm\right)\)
Đúng 0
Bình luận (0)
Câu 1: Cho tam giác đều có cạnh 60. Trên canh BC lấy điểm D sao cho BD=20. Đường trung trực của AD cắt AB tại E. Tính độ dài DE.
Xem chi tiết
Xét ΔBDA có \(cosB=\dfrac{BD^2+BA^2-AD^2}{2\cdot BD\cdot BA}\)
=>\(20^2+60^2-AD^2=2\cdot20\cdot60\cdot cos60=40\cdot60\cdot\dfrac{1}{2}=20\cdot60=1200\)
=>\(AD=\sqrt{20^2+60^2-1200}=20\sqrt{7}\left(cm\right)\)
Xét ΔBAD có \(\dfrac{BD}{sinBAD}=\dfrac{AD}{sinB}\)
=>\(\dfrac{20}{sinBAD}=\dfrac{20\sqrt{7}}{sin60}=\dfrac{40\sqrt{21}}{3}\)
=>\(\dfrac{1}{sinBAD}=\dfrac{2\sqrt{21}}{3}\)
=>\(sinBAD=\dfrac{3}{2\sqrt{21}}\)
=>góc BAD=19 độ
góc AED=180-2*19=142 độ
Xét ΔAED có AD/sinAED=DE/sinEAD
=>\(\dfrac{DE}{\dfrac{3}{2\sqrt{21}}}=\dfrac{20\sqrt{7}}{sin142}\)
=>\(DE\simeq28,13\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC, biết góc A vuông, góc B=48 độ, cạnh b=20. Độ dài cạnh a là:
Với các giả thiết câu của câu trên, độ dài cạnh c là:
Xét ΔABC vuông tại A
\(sinB=\dfrac{AC}{BC}\\ \Leftrightarrow\sin48=\dfrac{20}{a}\\\Leftrightarrow a=26,9\\BC^2=AC^2+AB^2\\ 29,6^2=20^2+c^2 \\ \Leftrightarrow c^2=476,16\\ \Leftrightarrow c=\sqrt{476,16}=21,8\)
Đúng 2
Bình luận (12)
Cho tam giác ABC vuông tại A , đường cao AH , biết AC = 13cm , ACB = 40° . TÍNH AB AC BC AH
Bài 1: Cho ∆ABC , BAC = 90° AC= 7cm, BC=15cm.Giải ∆ABC
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(AB^2=15^2-7^2=176\)
=>\(AB=4\sqrt{11}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AC}{BC}=\dfrac{7}{15}\)
=>\(\widehat{C}\simeq28^0\)
=>\(\widehat{B}=90^0-28^0=62^0\)
Đúng 2
Bình luận (0)
Bài 1: Cho tam giác ABC, A= 90 độ, B=30 độ AB= 8cm, Giải tam giác ABC bạn nhớ kẻ hình giúp tớ nhé
ΔABC vuông tại A
=>góc B+góc C=90 độ
=>góc C=60 độ
Xét ΔABC vuông tại A có \(cosB=\dfrac{AB}{BC}\)
=>8/BC=căn 3/2
=>BC=16/căn 3(cm)
=>\(AC=\dfrac{8}{\sqrt{3}}\left(cm\right)\)
Đúng 0
Bình luận (0)
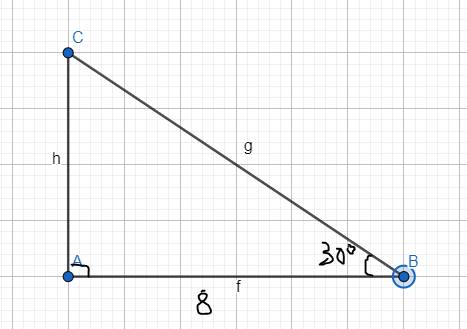
\(\widehat{C}=90^0-\widehat{B}=90^0-30^0=60^0\)
\(sin60=\dfrac{AB}{BC}=\dfrac{8}{BC}\Rightarrow BC=9,2\left(cm\right)\\ \sin30=\dfrac{AC}{BC}=\dfrac{AC}{9,2}\\ \Rightarrow AC=4,6\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A,kẻ đường cao AH AB=3cm,AC=4cm a)tính BC,AC b)tính góc BAH c)Chứng MINH BH=CH.tan2B
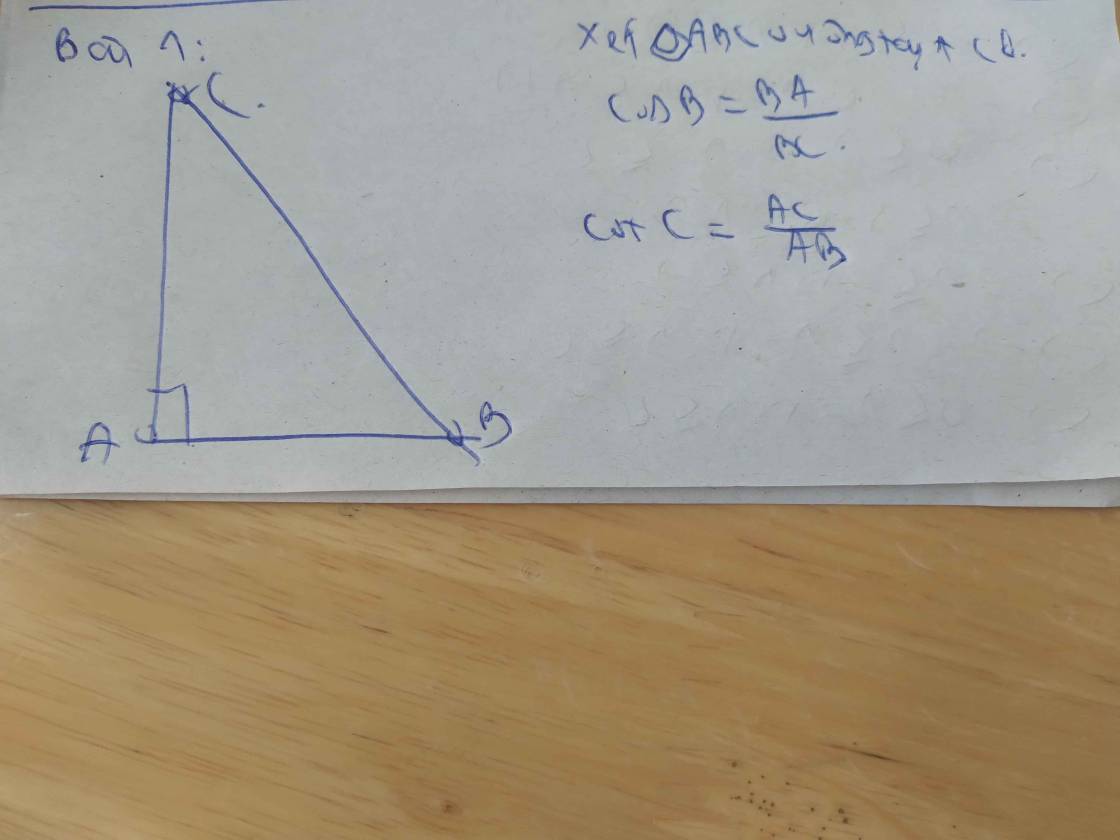
Cho tam giác ABC vuông tại A hãy viết các tỉ số lượng giác của góc B
Các tỉ số lượng giác của góc B là:
\(\left\{{}\begin{matrix}sinB=\dfrac{AC}{BC}\\cosB=\dfrac{AB}{BC}\\tanB=\dfrac{AC}{AB}\\cotB=\dfrac{AB}{AC}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Bài 1 : Cho tam giác ABC vuông tại A hãy viết tỉ số lượng giác CosB và cotC Bài 2 :. Cho tam giác ABC vuông tại A có đường cao AK chia cạnh huyền BC thành hai đoạn KB=3 cm và KC=9 cm a) Tỉnh độ dài các đoạn thẳng: BC,AB b) Tính độ dài đoạn thẳng AK c) Trên cạnh AC lấy điểm M ( M khác A và C ). Gọi H là hình chiếu cùa A trên BM. Chứng minh rằng BH .BM=BK . BC
Cho tam giác ABC vuông tại A
a) Biết cosC = 5/13. Tính sinC, cosB và tanC
b) Biết tanB = 1/5 . Tính E = sinB - 3cosB/2sinB + 3cosB
\(a,cosC=\dfrac{5}{13}\\ Ta,có:cos^2C+sin^2C=1\\ \Rightarrow sinC=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\\ cosB+sinC=1\\ \Leftrightarrow cosB+\dfrac{12}{13}=1\\ \Rightarrow cosB=\dfrac{1}{13}\\ tanC=\dfrac{sinC}{cosC}=\dfrac{\dfrac{12}{13}}{\dfrac{5}{13}}=\dfrac{12}{5}\)
Đúng 3
Bình luận (0)
\(b,tanB=\dfrac{1}{5}\Rightarrow\dfrac{sinB}{cosB}=\dfrac{1}{5}\Rightarrow cosB=5sinB\\ E=\dfrac{sinB-3cosB}{2sinB+3cosB}=\dfrac{sinB-3.5.sinB}{2sinB+3.5.sinB}=\dfrac{-14sinB}{17sinB}=-\dfrac{14}{17}\)
Đúng 1
Bình luận (0)