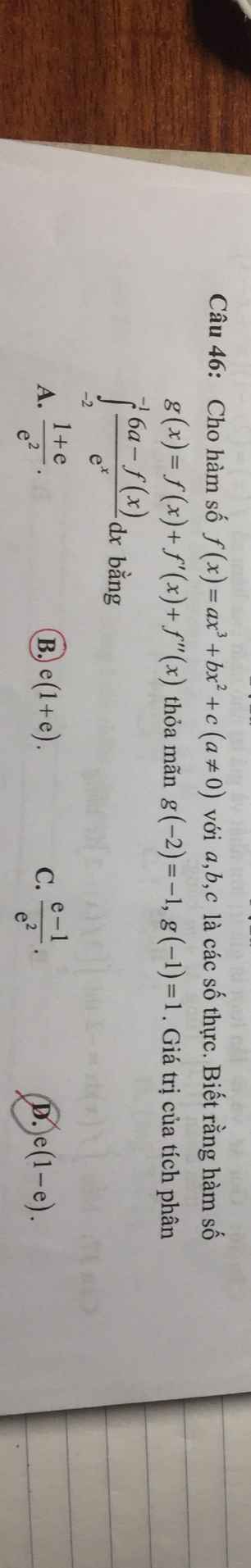Bài 4: Hàm số mũ. Hàm số logarit

Sau 6 tháng nhận được:

\(15.\left(1+\dfrac{5}{100}\right)=15,75\) triệu đồng

Sau 12 tháng nhận được:

\(15\left(1+\dfrac{5}{100}\right)^2=16,5375\) triệu đồng

Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) và viết đầy đủ yêu cầu đề để được hỗ trợ tốt hơn.

\(y'=\dfrac{-2-m}{\left(x-1\right)^2}.e^{\dfrac{2x+m}{x-1}}\) 

\(\Rightarrow\) Hàm đơn điệu trên miền xác định

TH1: \(\left\{{}\begin{matrix}-2-m< 0\\y\left(2\right)=e^5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>-2\\\dfrac{m+4}{1}=5\end{matrix}\right.\) \(\Rightarrow m=1\)

TH2: \(\left\{{}\begin{matrix}-2-m>0\\y\left(4\right)=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< -2\\\dfrac{m+8}{3}=5\end{matrix}\right.\) \(\Rightarrow\) ko tồn tại m thỏa mãn

Vậy \(m=1\)

\(\Leftrightarrow x^3-3x^2+m>0\) ; \(\forall x\in\left(1;3\right)\)

\(\Leftrightarrow x^3-3x^2>-m\) ; \(\forall x\in\left(1;3\right)\)

Xét hàm \(f\left(x\right)=x^3-3x^2\) trên \(\left(1;3\right)\)

\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

\(\Rightarrow\min\limits_{\left(1;3\right)}f\left(x\right)=f\left(2\right)=-4\)

\(\Rightarrow m< -4\)

\(I=\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx-\int\limits^{-1}_{-2}\dfrac{f\left(x\right)}{e^x}dx=J-I_1\)

Xét \(I_1\) , đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I_1=-f\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f'\left(x\right)}{e^x}dx=-f\left(-1\right).e+f\left(-2\right).e^2+I_2\)

Xét \(I_2\) , đặt \(\left\{{}\begin{matrix}u=f'\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f''\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I_2=-f'\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f''\left(x\right)}{e^x}dx=-f'\left(-1\right).e+f'\left(-2\right).e^2+I_3\)

Xét \(I_3\) , đặt \(\left\{{}\begin{matrix}u=f''\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'''\left(x\right)dx=6a.dx\\v=-e^{-x}\end{matrix}\right.\)

\(\Rightarrow I_3=-f''\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx=-f''\left(-1\right).e+f''\left(-2\right).e^2+J\)

Do đó:

\(I=J+f\left(-1\right).e-f\left(-2\right).e^2+f'\left(-1\right).e-f'\left(-2\right).e^2+f''\left(-1\right).e-f''\left(-2\right).e^2-J\)

\(=e\left[f\left(-1\right)+f'\left(-1\right)+f''\left(-1\right)\right]-e^2\left[f\left(-2\right)+f'\left(-2\right)+f''\left(-2\right)\right]\)

\(=e.g\left(-1\right)-e^2.g\left(-2\right)=e+e^2=e\left(e+1\right)\)

\(\int\limits^2_1f\left(x\right)=5\Rightarrow F\left(2\right)-F\left(1\right)=5\)

\(\Rightarrow F\left(2\right)=5+F\left(1\right)=5+1=6\)

`a)TXĐ: R`

`b)TXĐ: R\\{0}`

`c)TXĐ: R\\{1}`

`d)TXĐ: (-oo;-1)uu(1;+oo)`

`e)TXĐ: (-oo;-1/2)uu(1/2;+oo)`

`f)TXĐ: (-oo;-\sqrt{2})uu(\sqrt{2};+oo)`

`h)TXĐ: (-oo;0) uu(2;+oo)`

`k)TXĐ: R\\{1/2}`

`l)ĐK: {(x^2-1 > 0),(x-2 > 0),(x-1 ne 0):}`

`<=>{([(x > 1),(x < -1):}),(x > 2),(x ne 1):}`

`<=>x > 2`

   `=>TXĐ: (2;+oo)`