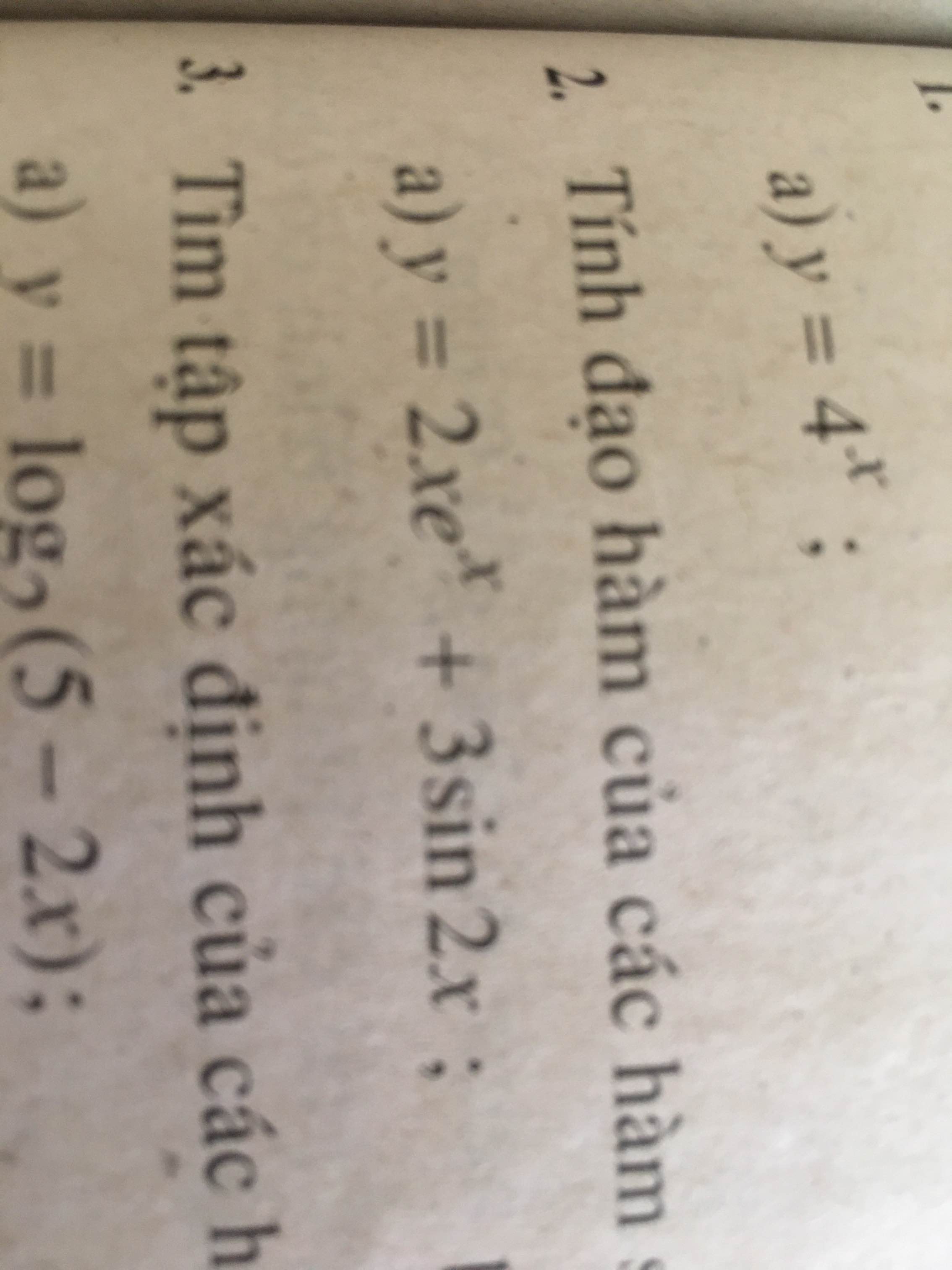Bài 4: Hàm số mũ. Hàm số logarit

\(\Leftrightarrow2^{-3}.2^{2x}-3.2^{-2}.2^x+1=0\)

\(\Leftrightarrow\dfrac{1}{8}2^{2x}-\dfrac{3}{4}2^x+1=0\)

Đặt \(2^x=t>0\)

\(\Rightarrow\dfrac{1}{8}t^2-\dfrac{3}{4}t+1=0\Rightarrow\left[{}\begin{matrix}t=4\\t=2\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}2^x=4\\2^x=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=2\\x=1\end{matrix}\right.\)

e là cái gì? tham số hả.

Giải biện luận, hay là sao mập mờ quá

\(A=\dfrac{1}{2}\left(e^x-e^{-x}\right)=\dfrac{1}{2}\left(e^x-\dfrac{1}{e^x}\right)\)

\(e^x-\dfrac{1}{e^x}=0\)

- nếu e =1 => đúng với x

-nếu e<0..{ phụ thuộc biến x chẵn , lẻ....khó quá}

xét e>0 e khác 1

đặt e^x=y=> y>0

\(y^2-1=0\Rightarrow y=1\)

\(e^x=1\Rightarrow x=0\)

1.

\(y'=\left(\dfrac{x}{lnx}\right)'.3^{\dfrac{x}{lnx}}.ln3=\dfrac{lnx-1}{ln^2x}.3^{\dfrac{x}{lnx}}.ln3\)

2.

\(y'=\left(tanx\right)'.tanx+\left(tanx\right)'.\dfrac{1}{tanx}=\dfrac{tanx}{cos^2x}+\dfrac{1}{tanx.cos^2x}\)

3.

\(y=\left(ln2x\right)^{\dfrac{2}{3}}\Rightarrow y'=\left(ln2x\right)'.\dfrac{2}{3}.\left(ln2x\right)^{-\dfrac{1}{3}}=\dfrac{1}{3x\sqrt[3]{ln2x}}\)

Giải:

Đặt \(2^x=a,3^x=b\)

PT trở thành \(3a^2-2ab=b^2\Leftrightarrow (a-b)(3a+b)=0\)

TH1: \(a=b\Rightarrow 2^x=3^x\). Hiển nhiên \(x=0\)

TH2: \(3a+b=0\Leftrightarrow 3.2^x+3^x=0\)

Điều này vô lý vì t biết rằng với \(a>0\) thì \(a^n>0\forall n\in\mathbb{R}\)

Vậy PT có \(x=0\) là nghiệm

Lời giải:

a)

Để hàm không có cực trị thì \(y'=3x^2-6x+3m=0\) không có nghiệm hoặc có nghiệm kép

\(\Leftrightarrow \Delta'=9-9m\leq 0\Leftrightarrow m\geq 1\)

b)

Để ĐTHS có điểm cực đại và cực tiểu thì

\(y'=3x^2-6x+3m=0\) phải có hai nghiệm phân biệt

\(\Leftrightarrow \Delta'=9-9m>0\Leftrightarrow m<1\)

có ai ko, giúp e với. chỉ e "đường đi" hoặc có bài giải càng tốt. pls!!

mún lấy đạo hàm mà tịt lun r. ko hỉu