Cho tam giác ABC có cạnh AB nhỏ hơn cạnh AC. Đường phân giac AD của góc BAC cắt BC tại D a.Biết BD=4cm.CD=6cm.Tính tỉ số AB/Ac b. Từ D vẽ đường thẳng song song với AB cắt AC tại E. Chứng minh rằng:AE. BC=AB.CD
Bài 3: Tính chất đường phân giác của tam giác
a: AB/AC=BD/CD=2/3
b: Xét ΔAED có \(\widehat{EAD}=\widehat{EDA}\)
nên ΔAED cân tại E
=>EA=ED
XétΔABC có DE//AB
nên CD/BC=DE/AB
=>CD/BC=EA/AB
hay \(CD\cdot AB=EA\cdot BC\)
Đúng 0
Bình luận (0)
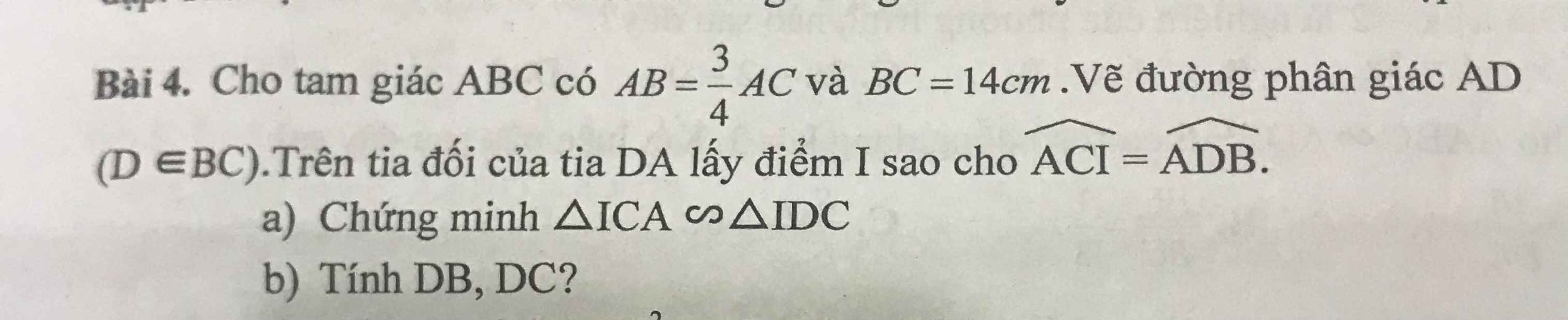
Làm giúp mình câu b với ạ. Mình xin cảm ơn
b: AD là phân giác
=>DB/AB=DC/AC
=>DB/DC=AB/AC=3/4
=>DB/3=DC/4
mà DB+DC=BC=14
nên DB/3=DC/4=14/7=2
=>DB=6cm; DC=8cm
Đúng 0
Bình luận (0)
Giúp mình với các bạn ^^
a: BC=căn 18^2+24^2=30cm
AD là phân giác
=>DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=30/7
=>DB=90/7cm; DC=120/7cm
b: Xét ΔECB có
CA,ED là đường cao
CA cắt ED tại F
=>F là trực tâm
=>BF vuông góc CE tại K
Xét ΔEKB vuông tại K và ΔEAC vuông tại A có
góc KEB chung
=>ΔEKB đồng dạng với ΔEAC
=>EK/EA=EB/EC
=>EK*EC=EA*EB
Đúng 0
Bình luận (0)
Cho tam giác ABC vuoong tại A,phân giác BE.Biết rằng BC=10cm,CE=5cm.Tính độ dài AB,AC
Xét ΔABC có BE là phân giác
nên AB/AE=BC/CE=2
=>AB=2AE
=>tan ABE=1/2
1+tan^2ABE=1/cos^2(ABE)
=>1/cos^2ABE=1+1/4=5/4
=>cos^2ABE=4/5
=>cos ABE=2/căn 5
cos ABC=cos (2*ABE)
\(=2\cdot\left(\dfrac{2}{\sqrt{5}}\right)^2-1=\dfrac{3}{5}\)
=>AB/BC=3/5
=>AB=6cm
=>AC=8cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=4cm,BC=5cm,CA=6cm.Goị G và I lầ lượt là trọng tâm và giao ba đường phân giác của tam giác.Tính độ dài IG
Cho tam giác ABC có AB=4cm,BC=5cm,CA=6cm.Goị G và I lầ lượt là trọng tâm và giao ba đường phân giác của tam giác.Tính độ dài IG
Giúp bài 4 với ạ
4:
a: MB/MC=AB/AC=3/4
b; Xét ΔCMN vuông tại M và ΔCAB vuông tại A có
góc C chung
=>ΔCMN đồng dạng vớiΔCAB
Đúng 0
Bình luận (0)
Giúp mình bài 4 với ah

Bài 5:
-Áp dụng BĐT AM-GM ta có:
\(\dfrac{\left(a+b\right)^2}{4}\ge ab>a+b\)
\(\Rightarrow\left(a+b\right)^2>4\left(a+b\right)\)
\(\Leftrightarrow\left(a+b\right)^2-4\left(a+b\right)>0\)
\(\Leftrightarrow\left(a+b\right)\left(a+b-4\right)>0\)
\(\Leftrightarrow a+b-4>0\) (do \(a+b>0\))
\(\Leftrightarrow a+b>4\) (đpcm)
Đúng 1
Bình luận (0)
Bài 4:
a) -△ABC có: AD là phân giác.
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{MB}{MC}\Rightarrow\dfrac{MB}{MC}=\dfrac{6}{8}=\dfrac{3}{4}\).
b) -△ABC và △MNC có: \(\widehat{BAC}=\widehat{NMC}=90^0;\widehat{ACB}\) là góc chung.
\(\Rightarrow\)△ABC∼△MNC (g-g).
c) -△ABC vuông tại A có: \(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(\dfrac{MB}{MC}=\dfrac{AB}{AC}\Rightarrow\dfrac{MB}{AB}=\dfrac{MC}{AC}=\dfrac{MB+MC}{AB+AC}=\dfrac{BC}{AB+AC}\)
\(\Rightarrow MC=\dfrac{BC.AC}{AB+AC}=\dfrac{10.8}{6+8}=\dfrac{40}{7}\left(cm\right)\)
△ABC∼△MNC\(\Rightarrow\dfrac{S_{ABC}}{S_{MNC}}=\left(\dfrac{AC}{MC}\right)^2=\dfrac{8}{\dfrac{40}{7}}=\dfrac{7}{5}\)
\(\Rightarrow S_{MNC}=\dfrac{5}{7}S_{ABC}=\dfrac{5}{7}.\dfrac{1}{2}.6.8=15\left(cm^2\right)\)
Đúng 1
Bình luận (1)
Cho tam giac CDE vuông tại C, có CD = 9cm, CE = 12cm, đường phân giác DM. a) Tính CM, CE. b)Vẽ MP ⊥ DE ( P ∈ DE). Tính diện tích tam giác PME.











