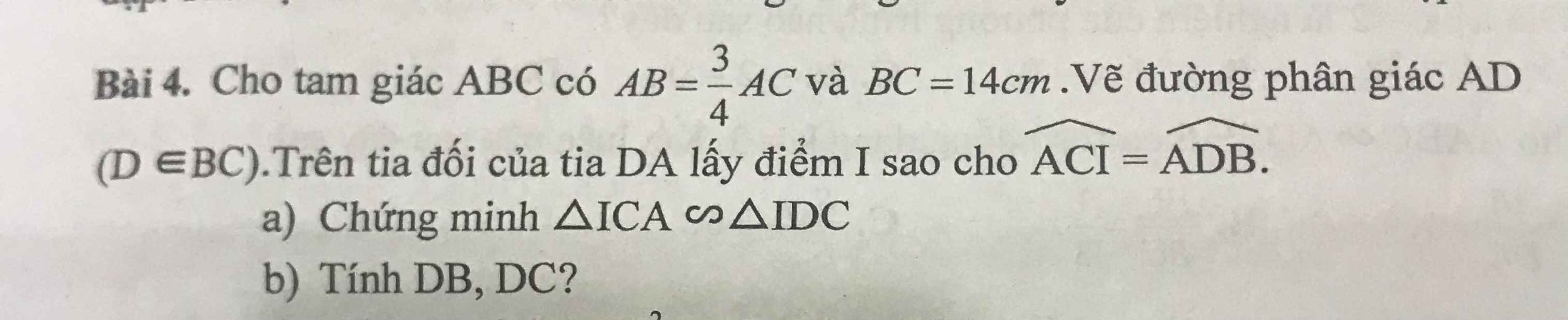Bài 5:
-Áp dụng BĐT AM-GM ta có:
\(\dfrac{\left(a+b\right)^2}{4}\ge ab>a+b\)
\(\Rightarrow\left(a+b\right)^2>4\left(a+b\right)\)
\(\Leftrightarrow\left(a+b\right)^2-4\left(a+b\right)>0\)
\(\Leftrightarrow\left(a+b\right)\left(a+b-4\right)>0\)
\(\Leftrightarrow a+b-4>0\) (do \(a+b>0\))
\(\Leftrightarrow a+b>4\) (đpcm)
Bài 4:
a) -△ABC có: AD là phân giác.
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{MB}{MC}\Rightarrow\dfrac{MB}{MC}=\dfrac{6}{8}=\dfrac{3}{4}\).
b) -△ABC và △MNC có: \(\widehat{BAC}=\widehat{NMC}=90^0;\widehat{ACB}\) là góc chung.
\(\Rightarrow\)△ABC∼△MNC (g-g).
c) -△ABC vuông tại A có: \(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(\dfrac{MB}{MC}=\dfrac{AB}{AC}\Rightarrow\dfrac{MB}{AB}=\dfrac{MC}{AC}=\dfrac{MB+MC}{AB+AC}=\dfrac{BC}{AB+AC}\)
\(\Rightarrow MC=\dfrac{BC.AC}{AB+AC}=\dfrac{10.8}{6+8}=\dfrac{40}{7}\left(cm\right)\)
△ABC∼△MNC\(\Rightarrow\dfrac{S_{ABC}}{S_{MNC}}=\left(\dfrac{AC}{MC}\right)^2=\dfrac{8}{\dfrac{40}{7}}=\dfrac{7}{5}\)
\(\Rightarrow S_{MNC}=\dfrac{5}{7}S_{ABC}=\dfrac{5}{7}.\dfrac{1}{2}.6.8=15\left(cm^2\right)\)