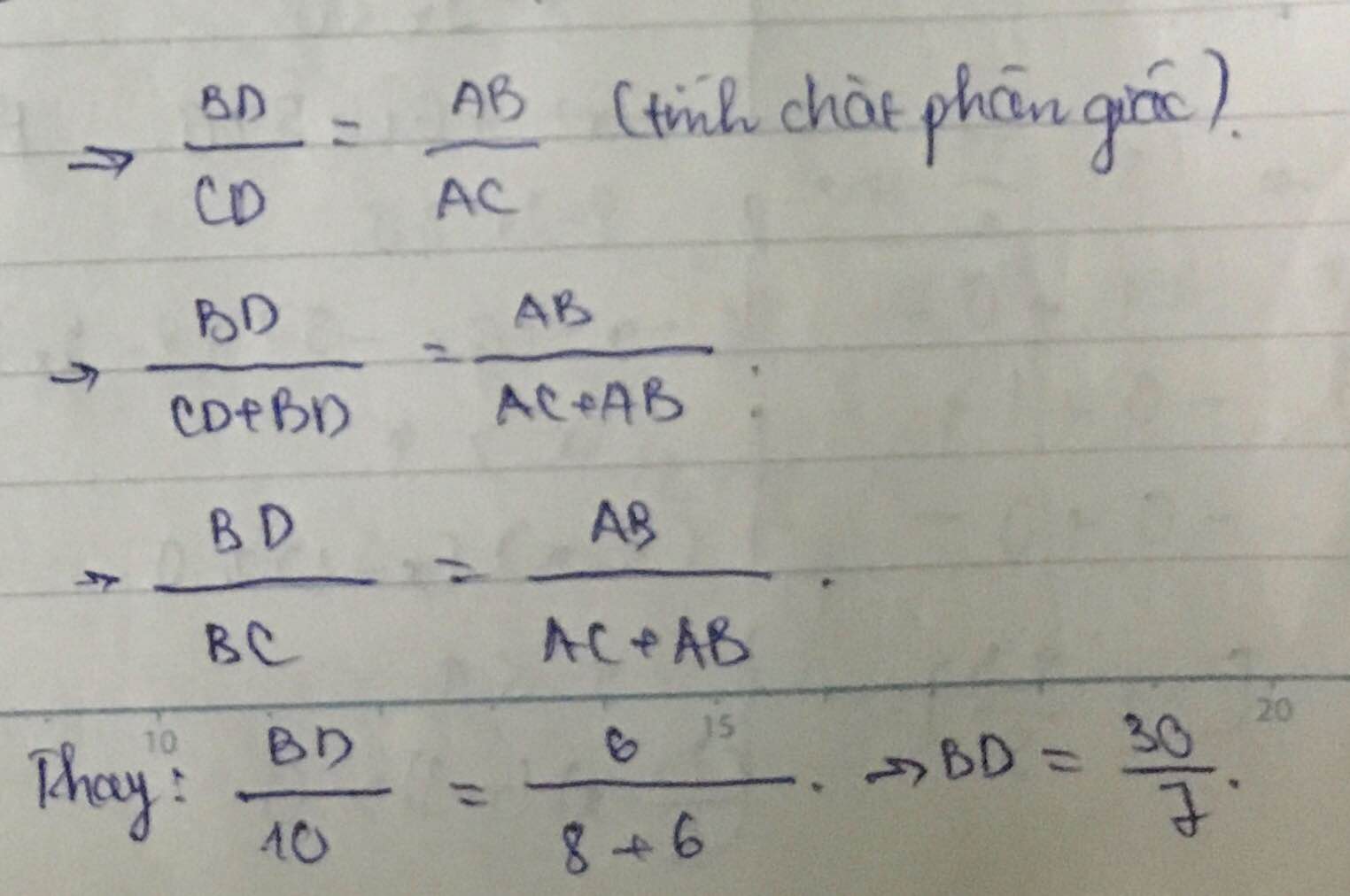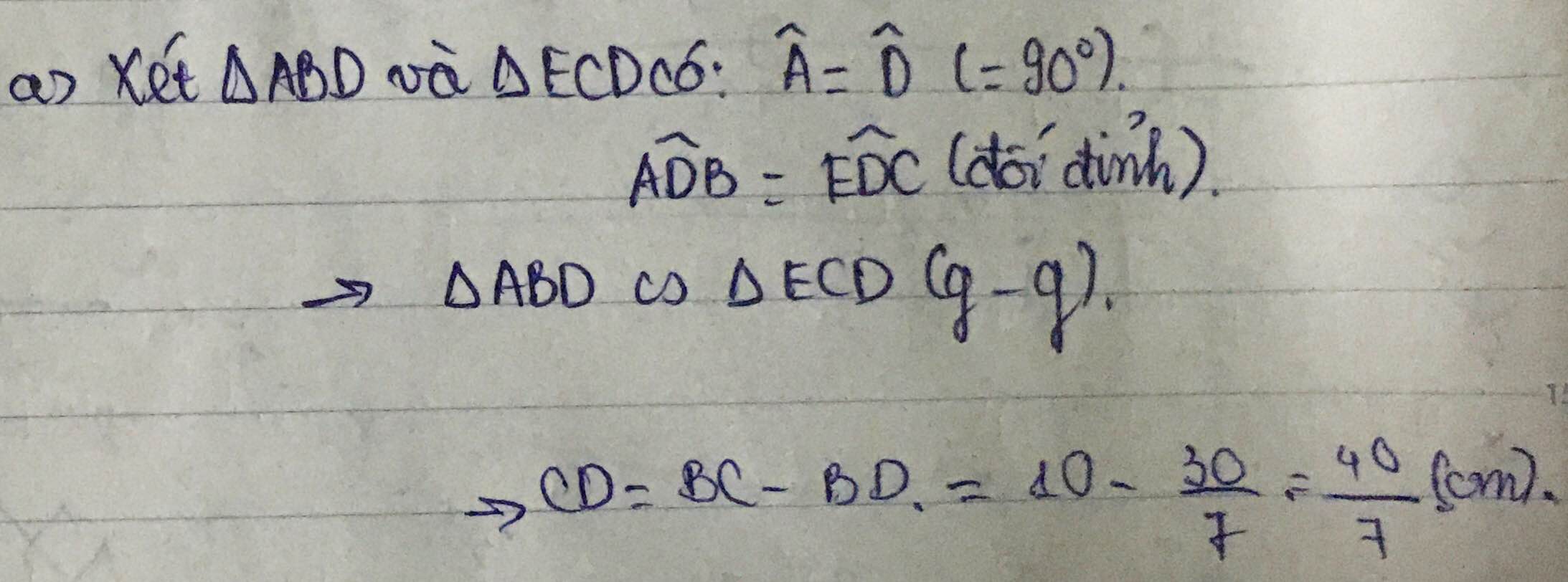Câu 2: cho tam giác ABC có AB= 10cm, AC = 35 cm. vẽ tia phân giác AD, trên AD lấy điểm E sao cho AE = ¾.AD, tia BE cắt AC tại I, tính độ dài AI
Bài 3: Tính chất đường phân giác của tam giác
-Qua D kẻ đường thẳng song song BI cắt AC tại F.
-Xét △ABC: AD là tia p/g của \(\widehat{BAC}\) (gt)
\(\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}\) (định lí đường phân giác trong tam giác)
\(\Rightarrow\dfrac{BD}{CD}=\dfrac{10}{35}=\dfrac{2}{7}\)
-Có: \(AE=\dfrac{3}{4}AD\) (gt) ; \(AE+ED=AD\)
\(\Rightarrow\dfrac{3}{4}AD+ED=AD\)
\(\Rightarrow ED=\dfrac{1}{4}AD\)
\(\Rightarrow\dfrac{AE}{ED}=\dfrac{\dfrac{3}{4}AD}{\dfrac{1}{4}AD}=3\)
-Xét △AIF: EI//DF.
\(\Rightarrow\dfrac{AI}{IF}=\dfrac{AE}{ED}=3\) (định lí Ta-let) (1) \(\Rightarrow IF=\dfrac{1}{3}AI\)
-Xét △IBC: DF//BI.
\(\Rightarrow\dfrac{IF}{CF}=\dfrac{BD}{CD}=\dfrac{2}{7}\) (định lí Ta-let) (2)
-Từ (1), (2) suy ra:
\(\dfrac{AI}{IF}.\dfrac{IF}{CF}=3.\dfrac{2}{7}=\dfrac{6}{7}\)
\(\Rightarrow\dfrac{AI}{CF}=\dfrac{6}{7}\)
\(\Rightarrow CF=\dfrac{7}{6}AI\)
*\(AI+IF+CF=AC\)
\(\Rightarrow AI+\dfrac{7}{6}AI+\dfrac{1}{3}AI=35\)
\(\Rightarrow\dfrac{5}{2}AI=35\)
\(\Rightarrow AI=14\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB=9 cm,AC=6cm,BC=10 cm.Tia phân giác của góc BAC cắt BC tại D.Tia phân giác góc ngoài của góc BAC cắt BC tại E.Tính đô dài đoạn DE.
GÍUP TỚ VỚI ,TỚ CẦN GẤP!!!!!!!!!
AD là phân giác trong của ΔABC
=>BD/AB=CD/AC
=>BD/9=CD/6=10/15
=>BD=90/15=6cm
AE làphân giác ngoài của ΔABC
=>EB/EC=AB/AC
=>EB/9=EC/6=(EB-EC)/(9-6)=10/3
=>EB=30/9cm; EC=20cm
ED=6-30/9=24/9=8/3(cm)
Đúng 0
Bình luận (0)
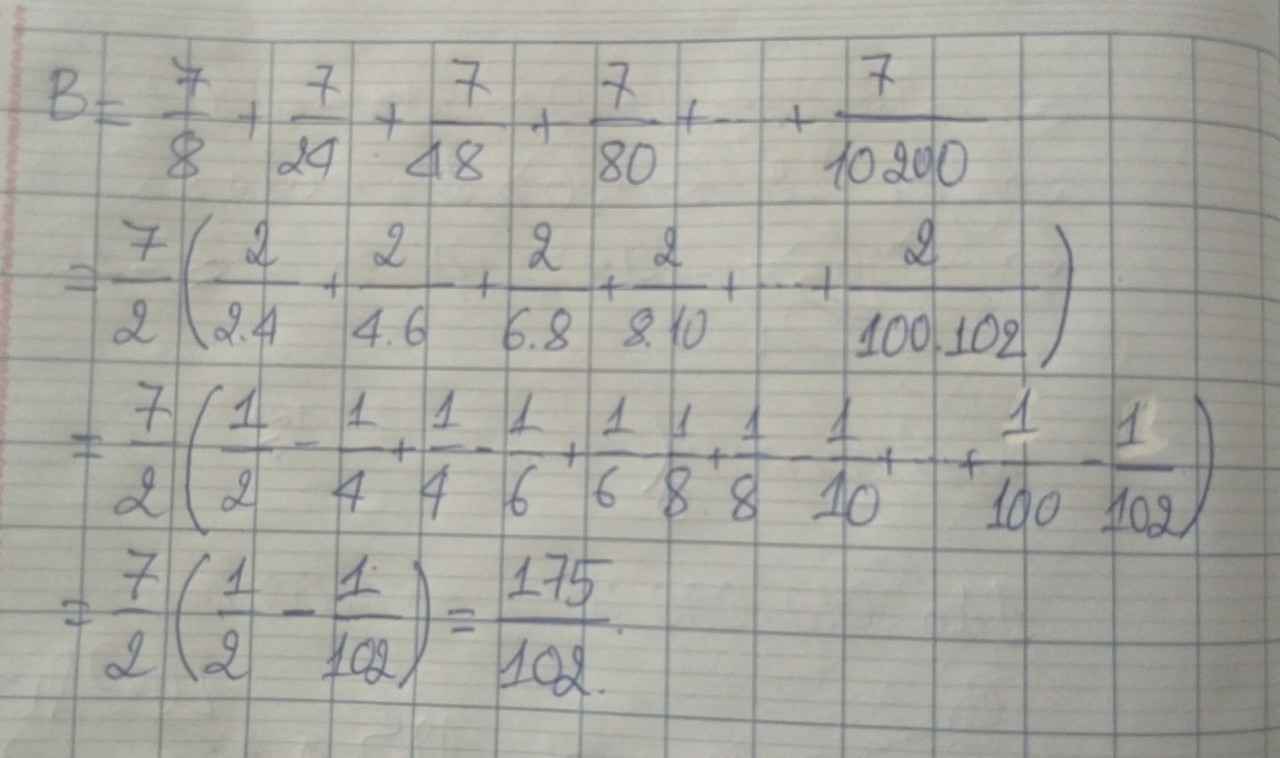
B=7/8+7/24+7/48+7/80+...+7/10200
Bài 16: Cho hình thang ABCD ( AB // CD), đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song
song với AB cắt các cạnh bên AD, BC lần lượt tại M, N.
1. Chứng minh: OM = ON 2. Chứng minh:
AM CN =1
AD CB
1: Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AM}{AD}\left(1\right)\)
Xét ΔBDC có ON//DC
nên \(\dfrac{ON}{DC}=\dfrac{BN}{BC}\left(2\right)\)
Xét hình thang ABCD có MN//AB//CD
nên \(\dfrac{AM}{MD}=\dfrac{BN}{NC}\)
=>\(\dfrac{MD}{AM}=\dfrac{CN}{NB}\)
=>\(\dfrac{MD+AM}{AM}=\dfrac{CN+NB}{NB}\)
=>\(\dfrac{AD}{AM}=\dfrac{CB}{BN}\)
=>\(\dfrac{AM}{AD}=\dfrac{NB}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{OM}{DC}=\dfrac{ON}{DC}\)
=>OM=ON
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AB=6cm, AC =8cm. Phân giác AD.
a)Tính độ dài BD và CD b) Kẻ DH vuông góc với AB. Tính DH, AD .
M.n giúp em với ạ ! Em c.ơn nhiều
Cho tam giác ABC vuông tại A , đường phân giác AD . Vẽ hình vuông MNPQ có M thuộc cạnh AB , N thuộc cạnh BC . Gọi E và F lần lượt là giao điểm của BN và MQ ; CM và NP. Chứng minh rằng :
a, DE song song với AC
b, DE=DF ; AE = AF
Cho tam giác nhọn ABC, BD và CE là 2 đng cao cắt nhau tại H.
a, CMR: \(\Delta\)HED ~ \(\Delta\)HBC
b,Gọi M là trung điểm của cạnh BC. Và P,Q lần lượt là hình chiếu của B, C trên đng thẳng ED. CM PE=QD.
a)Cho tam giác. Có thể lấy điểm D trên BC sao cho dfrac{BD}{AB} dfrac{DC}{AC} được không? Dự đoán vị trí điểm D.
b) Vẽ tam giác ABC thỏa mãn AB 2cm, AC 4cm, widehat{A} 800 (h.18)
- Dựng đường phân giác AD của góc A( bằng thước thẳng và compa)
- ĐO độ dài các đoạn thẳng BD và DC rồi so sánh các tỉ số dfrac{AB}{AC} và dfrac{DB}{DC}
c) Nhận xét :dfrac{AB}{AC}dfrac{DB}{DC}
Đọc tiếp
a)Cho tam giác. Có thể lấy điểm D trên BC sao cho \(\dfrac{BD}{AB}\)= \(\dfrac{DC}{AC}\) được không? Dự đoán vị trí điểm D.
b) Vẽ tam giác ABC thỏa mãn AB= 2cm, AC= 4cm, \(\widehat{A}\)= 800 (h.18)
- Dựng đường phân giác AD của góc A( bằng thước thẳng và compa)
- ĐO độ dài các đoạn thẳng BD và DC rồi so sánh các tỉ số \(\dfrac{AB}{AC}\) và \(\dfrac{DB}{DC}\)
c) Nhận xét :\(\dfrac{AB}{AC}\)=\(\dfrac{DB}{DC}\)
1.Tam giác ABC có độ dài các cạnh AB m, AC n và AD là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng mn.
2.Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC
3.Tam giác ABC có AB 5cm, AC 6cm, BC 7cm. Tia phân giác của góc BAC cắt BC tại E. Tính các đoạn EB, EC.
Đọc tiếp
|
1.Tam giác ABC có độ dài các cạnh AB= m, AC= n và AD là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng mn. 2.Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC 3.Tam giác ABC có AB= 5cm, AC= 6cm, BC= 7cm. Tia phân giác của góc BAC cắt BC tại E. Tính các đoạn EB, EC. |
Bài này mình có làm ở trong câu hỏi kia rồi nha
bạn vô đó tham khảo chứ mình ko viết đc 2 lần ra đâu :(
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A có đường phân giác AD.Biết rằng độ dài của các cạnh góc vuông AB = 3,75cm, AC = 4,5cm. Tính độ dài BD, CD
Xét tg ABC ( ^A = 90o ) có:
BC2 = AB2 + AC2 (định lý Pytago)
Thay số: BC2 = 3,752 + 4,52
BC2 = 14,0625 + 20,25
BC2 = 34,3125
BC = \(\sqrt{34,3125}\) (BC > 0)
Xét tg ABC có D là đường pg ^A ( gt )
=> \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
<=> \(\dfrac{AB}{AC+AB}=\dfrac{BD}{CD+BD}\)
Thay số: \(\dfrac{3,75}{4,5+3,75}=\dfrac{BD}{BC}\)
<=> \(\dfrac{3,75}{8,25}=\dfrac{BD}{\sqrt{34,3125}}\)
=> BD = (cm)
=> CD = BC - CD = (cm)
Đúng 1
Bình luận (0)