Question

Tam giác ABC vuông tại A có đường phân giác AD.Biết rằng độ dài của các cạnh góc vuông AB = 3,75cm, AC = 4,5cm. Tính độ dài BD, CD

Answer 1

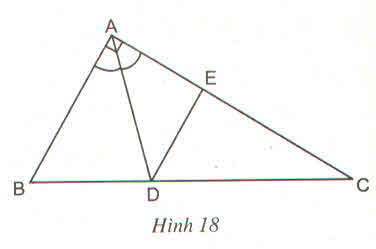
Xét tg ABC ( ^A = 90^o ) có:

                BC² = AB² + AC² (định lý Pytago)

Thay số:  BC² = 3,75² + 4,5²

                    BC² = 14,0625 + 20,25

                 BC² = 34,3125

                 BC = \(\sqrt{34,3125}\) (BC > 0)

Xét tg ABC có D là đường pg ^A ( gt )

=>            \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)

<=>        \(\dfrac{AB}{AC+AB}=\dfrac{BD}{CD+BD}\)

Thay số: \(\dfrac{3,75}{4,5+3,75}=\dfrac{BD}{BC}\)

<=>        \(\dfrac{3,75}{8,25}=\dfrac{BD}{\sqrt{34,3125}}\)   

=> BD =      (cm)

=> CD = BC - CD =        (cm)

 

Answer 2