Bài 2: Hai tam giác bằng nhau

Tính được các cạnh:

+ HI = AB = 2cm

+ IK = BC = 4cm

Tính được các góc:

+ góc I = góc B = 40 độ

Tam giác ABC = Tam giác IKH

Phần sau mình chưa học

ý b)...............cắt BD tại K

Kí hiệu trên hình vẽ đúng không bạn . Mình sẽ kí hiệu trên hình vẽ nhé chứ các cạnh và góc đề đã cho rồi .

toán lj có thơ và bài hát hả b

\(\Delta ABC=\Delta DEH\left(gt\right)\)

\(\Rightarrow AB=DE\) ( 2 cạnh tương ứng ) mà \(AB=5cm\)

\(\Rightarrow DE=5cm\)

\(AC=DH\)( 2 cạnh tương ứng ) mà \(AC=6cm\)

\(\Rightarrow DH=6cm\)

\(S_{DEH}=19\)

\(DE+DH+EH=19\)

\(5+9+EH=19\)

\(EH=19-9-5\)

\(EH=5cm\)

Chúc bạn học tốt!

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

Để kí hiệu sự bằng nhau của ΔABC và ΔA’B’C’ ta viết:

∆ABC= ∆A’B’C’.

∆ABC= ∆A’B’C’ nếu

Bài 10. Trong các hình sau các Δ nào bằng nhau(Các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các Δ bằng nhau đó. Viết kí hiệu về sự bằng nhau của các Δ đó.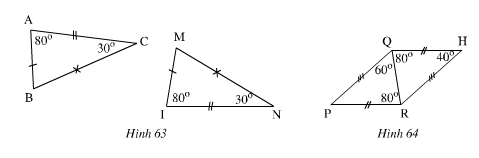

Hình 63:

Ta có:

Xét ΔABC ta có: ∠B =1800 – (∠A+∠C)=1800 – (800+300) =700

Xét ΔMIN ta có: ∠M =1800 – (∠I+∠N)=1800 – (800+300) =700

Và AB=MI, AC=IN, BC=MN.

nên ∆ABC = ∆IMN

Hình 64:

Ta có:

∠RQH = ∠QRP = 800 (ở vị trí so le trong)

Nên QH // RP

Nên ∠HRQ = ∠PQR = 600(so le trong)

∠P = ∠H = 400

và QH= RP, HR= PQ, QR chung.

nên ∆HQR = ∆PRQ.

Bài 11. Cho ∆ ABC = ∆ HIK

a) Tìm cạnh tương ứng với cạnh BC. Tìm góc tương ứng với ∠H

b) Tìm các cạnh bằng nhau, tìm các góc bằng nhau.

HD: a) Ta có ∆ ABC = ∆ HIK, nên cạnh tương ứng với BC là cạnh IK. Góc tương ứng với ∠H là ∠A.

b) ∆ ABC= ∆ HIK

Suy ra: AB = HI, AC = HK, BC = IK.
∠A = ∠H, ∠B =∠I, ∠C = ∠K.

Bài 12 trang 112. Cho ∆ ABC= ∆ HIK trong đó cạnh AB = 2cm. ∠B=400; BC= 4cm. Em có thể suy ra số đo của những cạnh nào, những góc nào của ΔHIK?

Ta có ∆ ABC= ∆ HIK (gt)

Suy ra: AB = HI= 2cm, BC = IK= 4cm, ∠I = ∠B = 400

Bài 13. Cho ∆ ABC= ∆ DEF. Tính chu vi mỗi tam giá nói trên biết AB = 4cm, BC = 6cm, DF = 5cm (chu vi của một tam giác là tổng độ dài ba cạnh của tam giác đó)

Ta có ∆ABC = ∆ DEF

Suy ra: AB = DE= 4cm, BC = EF = 6cm, DF = AC = 5cm.

Chu vi của ΔABC bằng: AB + BC + AC = 4 + 5 + 6 = 15 (cm)

Chu vi của ΔDEF bằng: DE + EF + DF = 4 + 5 + 6 = 15 (cm )

Bài 14 trang 112. Cho hai tam giác bằng nhau: ΔABC (Không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) và một Δ có ba đỉnh H, I ,K. Viết kí hiệu về sự bằng nhau của hai Δ đó biết: AB=KI, ∠B =∠K.

Giải: Ta có: ∠B =∠K nên B, K là hai đỉnh tương ứng.

AB= KI nên A, I là hai đỉnh tương ứng.

Vậy ∆ABC = ∆IKH.

a: Ta có: MA=MB

nên M nằm trên đường trung trực của AB(1)

Ta có: PA=PB

nên P nằm trên đường trung trực của AB(2)

Ta có: NA=NB

nên N nằm trên đường trung trực của AB(3)

Từ (1), (2) và (3) suy ra M,P,N thẳng hàng

b: Xét ΔMAP và ΔMBP có

MA=MB

PA=PB

MP chung

Do đó: ΔMAP=ΔMBP

Suy ra: \(\widehat{MAP}=\widehat{MBP}\)

c: Xét ΔMAN và ΔMBN có

MA=MB

NA=NB

MN chung

Do đó: ΔMAN=ΔMBN

Suy ra: \(\widehat{MAN}=\widehat{MBN}\)