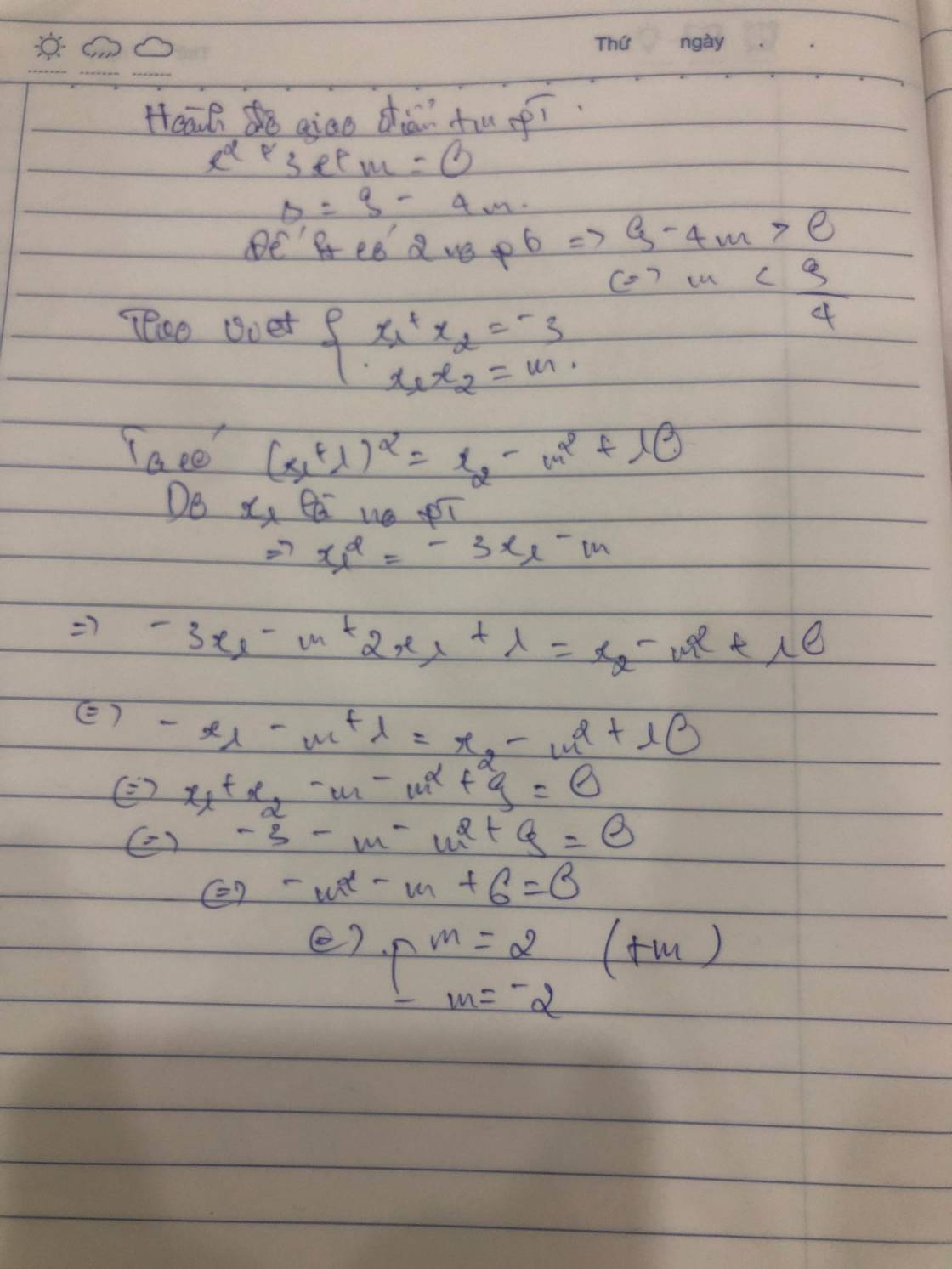Các câu hỏi tương tự
trong mặt phẳng tọa độ Oxy
(d):y=2x-m+1 và parabol (P):y=`1/2 x^2`
Tìm m để (d) cắt (P) tại 2 điểm phân biệt có tọa độ \(\left(x_1;y_1\right),\left(x_2;y_2\right)\) sao cho \(x_1x_2\left(y_1+y_2\right)+48=0\)
Cho (P): \(y=x^2\) và (d): \(y=mx-m+1\)
a. Tìm m để (d) cắt (P) tại 2 điểm phân biệt.
b. Tìm m để (d) cắt (P) tại 2 điểm phân biệt có hoành độ \(x_1,x_2\) thỏa mãn
\(A=\dfrac{2x_1x_2}{x_1^2+x_2^2+2\left(1+x_1x_2\right)}+2016\) đạt max, min
Làm câu (b) giúp em với ạ em cảm ơn nhiều
Cho (P): y =\(x^2\)
(d): y = 2x + 2m - 1
Tìm các giá trị của m để (P) và (d) cắt nhau tại 2 điểm phân biết có hoành độ \(x_1\), \(x_2\). thỏa mãn: \(x_2^2\left(x_1^2-1\right)+x_1^2\left(x^2_2-1\right)=8\)
Cho đường thẳng (d) : \(y=3x+m^2-1\) và \(\left(P\right):y=x^2\)
a) Chứng minh rằng : (d) luôn cắt ( P) tại 2 điểm phân biệt với mọi m
b) Gọi \(x_1,x_2\) là hoành độ các giao điểm của (d) và (P). Tìm m để \(\left(x_1+1\right)\left(x_2+1\right)=1\)
cho Parabol (P):y=`x^2`, (d):y=mx-m+2. Tìm m để (d) cắt (P) ở 2 điểm phân biệt \(M\left(x_1;y_1\right)\) và \(N\left(x_2;y_2\right)\) thỏa mãn \(x_1y_2+x_2y_1-15=0\)
Cho đường thẳng (d): \(y=\left(m+2\right)x-2m\) và parabol (P): \(y=x^2\)
a, Tìm m để đường thẳng (d) và parabol (P) cắt nhau tại hai điểm phân biệt
b, Gọi \(x_1\),\(x_2\) là hoành độ các giao điểm. Tìm m sao cho \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=\dfrac{5}{2}\)
Tìm m để phương trình: \(3x^2+4\left(m-1\right)x+m^2-4m+1=0\) có hai nghiệm phân biệt \(x_1,x_2\) thỏa mãn: \(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{1}{2}\left(x_1+x_2\right)\)
Trong mặt phẳng tọa độ Oxy cho đường thẳng (d):y=2x-2m+2 và parabol (P):y=x^2
a,Xác định các tọa độ giao điiểm của parabol (P)tại 2 điểm (d) khi m=-1/2
b,Tìm m để đường thẳng (d) vắt parabol (P) tại 2 điểm phân biệt \(A\left(x;y\right);B\left(x_2;y_2\right)\) sao cho \(y_1+y_2=4\left(x_1+x_2\right)\)
\(x^2-2\left(m+1\right)x+m^2+2=0\left(1\right)\)
tìm m để (1) có 2 nghiệm phân biệt `x_1 ,x_2` thỏa mãn \(x_1^2+2\left(m+1\right)x_2=12m+2\)
Cho parabol (P) \(y=x^2\) và đường thẳng (d): \(y=mx+4\)
a) Chứng tỏ đường thẳng (d) luôn cắt (P) tại 2 điểm phân biệt A; B. Gọi x1 ; x2 là hoành độ của A; B. Tìm MAX Q= \(\frac{2.\left(x_1+x_2\right)+7}{\left(x_1\right)^2+\left(x_2\right)^2}\)
b) Tìm m để SOAB= 8