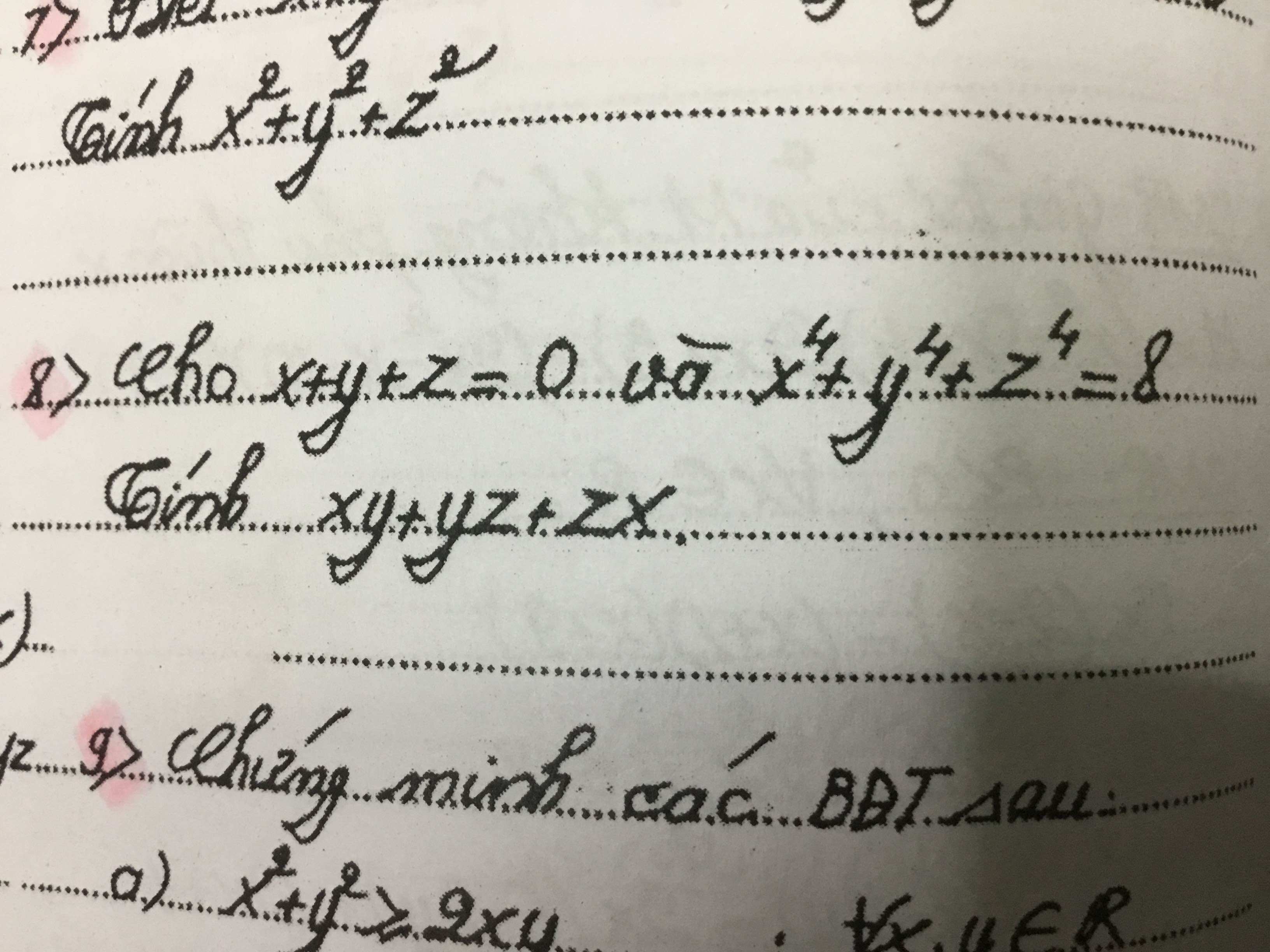Question

x+y+z=0 và x^4+y^4+z^4=8

Tính xy + yz +zx 

 

Answer 1

Lời giải:

$x^4+y^4+z^4=8$

$\Leftrightarrow (x^2+y^2+z^2)^2-2(x^2y^2+y^2z^2+z^2x^2)=8$

$\Leftrightarrow [(x+y+z)^2-2(xy+yz+xz)]^2-2[(xy+yz+xz)^2-2xyz(x+y+z)]=8$

$\Leftrightarrow [0^2-2(xy+yz+xz)]^2-2[(xy+yz+xz)^2-2xyz.0]=8$

$\Leftrightarrow 4(xy+yz+xz)^2-2(xy+yz+xz)^2=8$

$\Leftrightarrow 2(xy+yz+xz)^2=8$

$\Leftrightarrow (xy+yz+xz)^2=4$

$\Leftrightarrow xy+yz+xz=\pm 2$

Lại có:

$x+y+z=0$
$\Rightarrow (x+y+z)^2=0$

$\Leftrightarrow xy+yz+xz=\frac{-(x^2+y^2+z^2)}{2}\leq 0$

$\RIghtarrow xy+yz+xz=-2$