xí nghiệp A sản xuất độc quyền một loại sản phẩm. Biết rằng hàm tổng chi phí sản xuất là \(TC=x^3-77x^2+1000x+40000\) và hàm doanh thu là \(TR=-2x^2+1312x\) với x là số sản phẩm. Lợi nhuận của xí nghiệp A được xác định bằng hàm số \(f\left(x\right)=TR-TC\), cực đại lợi nhuận xí nghiệp A khi đó đạt bao nhiêu sản phẩm
\(f\left(x\right)=T\left(R\right)-T\left(C\right)=-2x^2+1312x-\left(x^3-77x^2+1000x+40000\right)\\ =-x^3+75x^2+312x-40000\)
Có: \(f'\left(x\right)=-3x^2+150x+312\)
+) \(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=52\left(n\right)\\x=-2\left(l\right)\end{matrix}\right.\)
BBT:
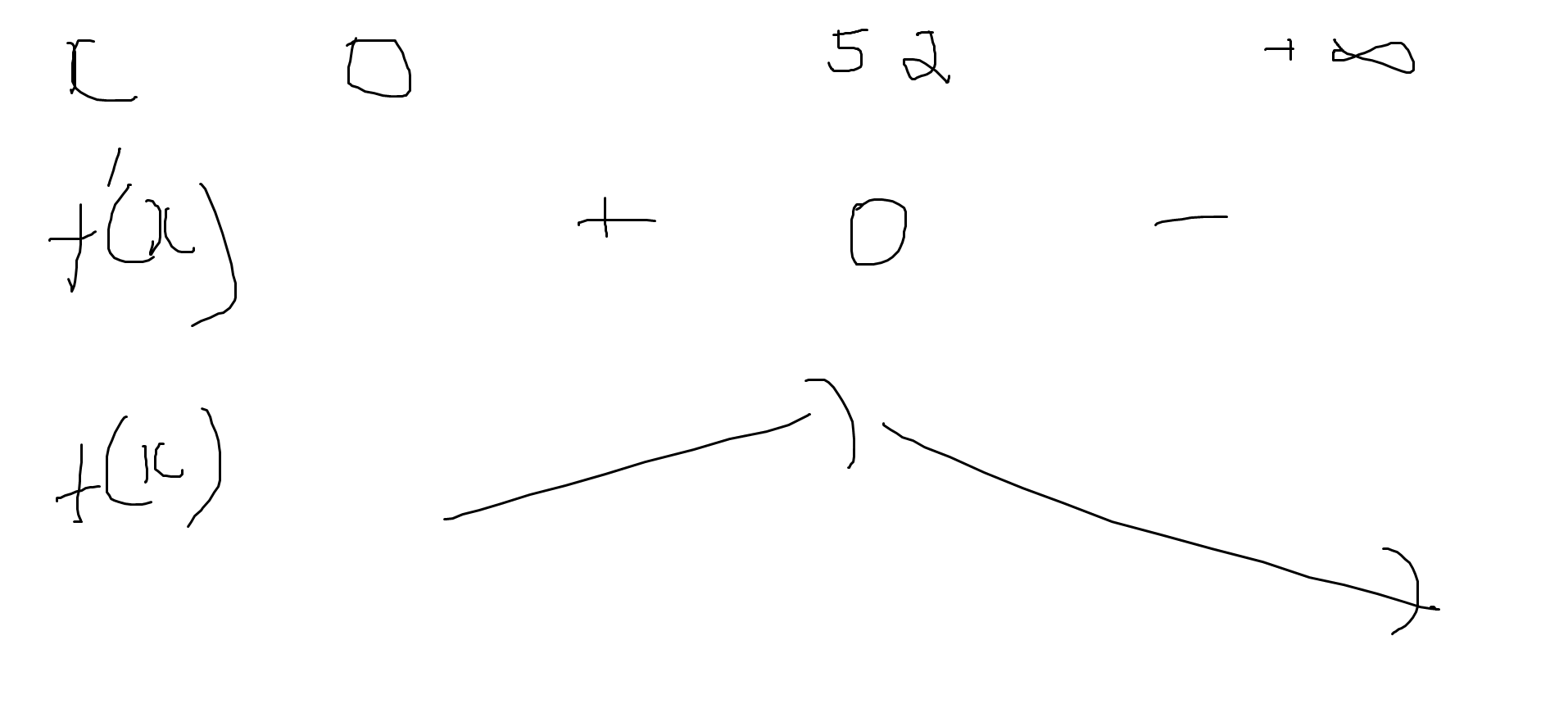
Lợi nhuận lớn nhất khi xí nghiệp A sản xuất 52 sản phẩm










