Các câu hỏi tương tự
Xét sự biến thiên của hàm số f(x)=x+1x1x trên khoảng (1; dương vô cực). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng (1; dương vô cực)
B. Hàm số nghịch biến trên khoảng (1; dương vô cực)
C. Hàm số đồng biến trên khoảng (-1;1)
D. Hàm số nghịch biến trên khoảng (âm vô cực; 1)
Mọi người giải ra giúp mình với ạ
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
Xét tính đồng biến, nghịch biến của hàm số f(x) x − 3x + 5 trên khoảng (−
∞
; −5) và trên khoảng (−5; +
∞
). Khẳng định nào sau đây đúng? A. Hàm số nghịch biến trên (−
∞
; −5), đồng biến trên (−5; +
∞
). B. Hàm số đồng biến trên (−
∞
; −5), nghịch biến trên (−5; +
∞
). C. Hàm số nghịch biến trên các khoảng (−
∞
; −5) và (−5; +
∞...
Đọc tiếp
Xét tính đồng biến, nghịch biến của hàm số f(x) = x − 3x + 5 trên khoảng (− ∞ ; −5) và trên khoảng (−5; + ∞ ). Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên (− ∞ ; −5), đồng biến trên (−5; + ∞ ).
B. Hàm số đồng biến trên (− ∞ ; −5), nghịch biến trên (−5; + ∞ ).
C. Hàm số nghịch biến trên các khoảng (− ∞ ; −5) và (−5; + ∞ ).
D. Hàm số đồng biến trên các khoảng (− ∞ ; −5) và (−5; + ∞ )
Xét tính đồng biến, nghịch biến của hàm số f(x)
x
2
−
4
x
+
5
trên khoảng (−
∞
; 2) và trên khoảng (2; +
∞
). Khẳng định nào sau đây đúng? A. Hàm số nghịch biến trên (−
∞
; 2), đồng biến trên (2; +
∞
). B. Hàm số đồng biến trên (−
∞
; 2), nghịch biến trên (2; +...
Đọc tiếp
Xét tính đồng biến, nghịch biến của hàm số f(x) = x 2 − 4 x + 5 trên khoảng (− ∞ ; 2) và trên khoảng (2; + ∞ ). Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên (− ∞ ; 2), đồng biến trên (2; + ∞ ).
B. Hàm số đồng biến trên (− ∞ ; 2), nghịch biến trên (2; + ∞ ).
C. Hàm số nghịch biến trên các khoảng (− ∞ ; 2) và (2; + ∞ ).
D. Hàm số đồng biến trên các khoảng (− ∞ ; 2) và (2; + ∞ ).
Cho hàm số như trong ảnh có đồ thị là (C)
1, số giao điểm của đồ thị với trục hoành
2, lập bảng biến thiên nên khoảng đồng biến, nghịch biến của hàm số f(x)
Giúp em với ạ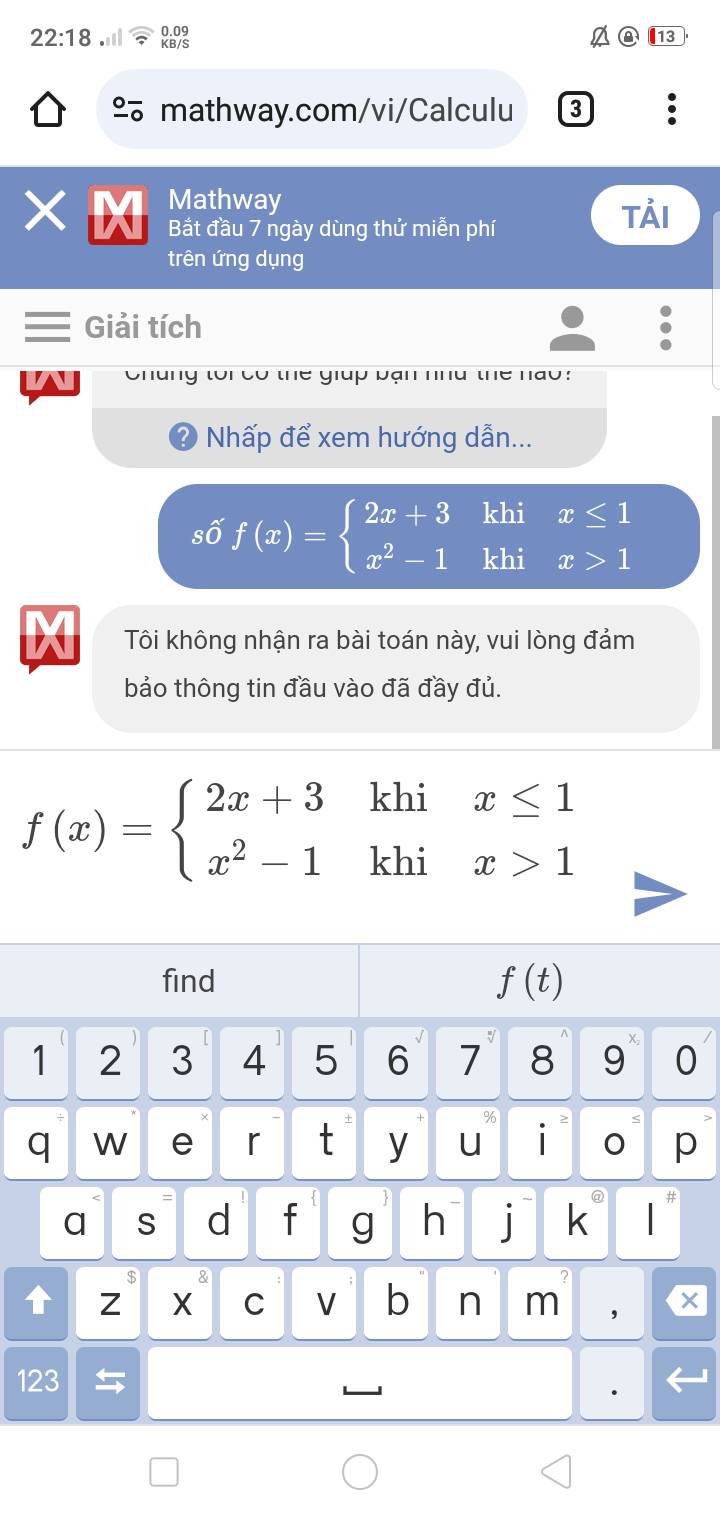
Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng
y = x 2 + 10 x + 9 t r ê n ( - 5 ; + ∞ )
Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng
y = - 1 1 + x trên (-3; 2) và (2; 3)
với giá trị nào của m thì hàm số sau đồng biến / nghịch biến trên (-∞, +∞)
a) y = (2m+5)x + m + 3
b) y = mx - 3 - x
Cho hàm số y=f(x) = 4x^2+ 6x-5 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×). b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]







