Các câu hỏi tương tự
Xét dãy
u
n
:
u
n
n
+
100
+
100
-
n
với n là các số tự nhiên nhỏ hơn hoặc bằng 100, số α dương nhỏ nhất thoả mãn
u
n
≤
α
là A. α10 B.
α
10
2
C. α11...
Đọc tiếp
Xét dãy u n : u n = n + 100 + 100 - n
với n là các số tự nhiên nhỏ hơn hoặc bằng 100, số α dương nhỏ nhất thoả mãn u n ≤ α là
A. α=10
B. α = 10 2
C. α=11
D. α=20
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:46
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
Cho góc
α
thỏa mãn
π
α
3
π
2
và sin
α
-2cos
α
1.Tính A 2tan
α
-cot
α
A. 6 B.
1
6
C. 2 D.
1
2
Đọc tiếp
Cho góc α thỏa mãn π < α < 3 π 2 và sin α -2cos α =1.Tính A= 2tan α -cot α
A. 6
B. 1 6
C. 2
D. 1 2
Cho hình chóp tứ giác S.ABCD. Gọi M, N là trung điểm của AB và BC. Mặt phẳng (α) thay đổi luôn đi qua MN cắt SC, SA tại P và Q
1-Tìm giao điểm của AD và SD với (α)
2-Tìm thiết diện của hình chóp bị cắt bởi (α)
3-Chứng minh rằng nếu thì 3 điểm S, B ,I thẳng hàng
Cho mặt phẳng (α) và hai đường thẳng a, b. Các mệnh đề sau đây đúng hay sai?
a) Nếu a // (α), b ⊥(α) thì a ⊥b.
b) Nếu a // (α), b ⊥a thì b ⊥(α).
c) Nếu a // (α), b // (α) thì b // a.
d) Nếu a ⊥(α), b ⊥a thì b ⊥(α).
Cho góc
α
thỏa mãn
π
α
3
π
2
và
sinα
-
2
cosα
1
Tính A
2
tan
α
-
c
o
t
α
Đọc tiếp
Cho góc α thỏa mãn π < α < 3 π 2 và sinα - 2 cosα = 1
Tính A= 2 tan α - c o t α
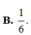
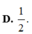
Cho hàm số �:[�;�]→[�;�]f:[a;b]→[a;b] liên tục trên [�,�][a,b] với ��ab thỏa mãn ∣�(�)−�(�)∣∣�−�∣∣f(α)−f(β)∣∣α−β∣, ∀�,�∈[�;�]∀α,β∈[a;b] phân biệt. Chứng minh rằng ∃!�∈[�;�]:�(�)�∃!γ∈[a;b]:f(γ)γ
(Ở đây kí hiệu ∃!∃! nghĩa là tồn tại duy nhất)
#Toán lớp 11
Đọc tiếp
Cho hàm số liên tục trên với thỏa mãn , phân biệt. Chứng minh rằng
(Ở đây kí hiệu nghĩa là tồn tại duy nhất)
#Toán lớp 11Cho hình chóp S.ABCD, M và N là hai điểm thuộc cạnh AB và CD, (α) là mặt phẳng qua MN và song song với SA. Thiết diện của hình chóp S.ABCD khi cắt bởi (α) là hình gì?
A. Tam giác
B. tứ giác
C. hình thang
D. hình bình hành
Cho dãy số
(
b
n
)
có số hạng tổng quát là
b
n
sin
α
+
sin
2
α
+
.
.
.
+
sin
n
α
với
α
≠
...
Đọc tiếp
Cho dãy số ( b n ) có số hạng tổng quát là b n = sin α + sin 2 α + . . . + sin n α với α ≠ π / 2 + k π . Tìm giới hạn của ( b n )