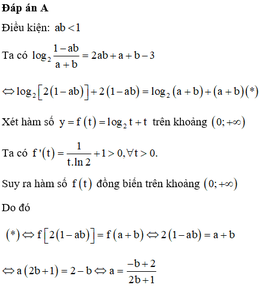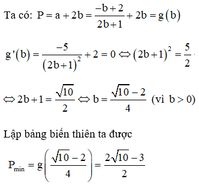Các câu hỏi tương tự
Xét các số thực dương a, b thỏa mãn
log
2
1
−
ab
a
+
b
2
ab
+
a
+
b
−
3
. Tìm giá trị nhỏ nhất
P
min...
Đọc tiếp
Xét các số thực dương a, b thỏa mãn log 2 1 − ab a + b = 2 ab + a + b − 3 . Tìm giá trị nhỏ nhất P min của P = a + 2 b
A. P min = 2 10 − 3 2 .
B. P min = 3 10 − 7 2 .
C. P min = 2 10 − 1 2 .
D. P min = 2 10 − 5 2 .
Cho số phức z thỏa mãn
z
-
1
+
3
i
+
z
¯
+
5
+
i
2
65
. Giá trị nhỏ nhất của
z
+
2
+
i...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 + 3 i + z ¯ + 5 + i = 2 65 . Giá trị nhỏ nhất của z + 2 + i đạt được khi z = a + b i với a, b là các số thực dương. Giá trị của 2 b + 3 a bằng
A. 19
B. 16
C. 24
D. 13
Cho các số thực a, b, m, n sao cho
2
m
+
n
0
và thỏa mãn điều kiện
log
2
a
2
+
b
2
+...
Đọc tiếp
Cho các số thực a, b, m, n sao cho 2 m + n < 0 và thỏa mãn điều kiện log 2 a 2 + b 2 + 9 = 1 + log 2 3 a + 2 b 9 − m .3 − n .3 − 4 2 m + n + ln 2 m + n + 2 2 + 1 = 81
Tìm giá trị nhỏ nhất của biểu thức P = a − m 2 + b − n 2
A. 2 5 − 2.
B. 2.
C. 5 − 2.
D. 2 5 .
Xét các số phức z a + bi, (a,b
∈
R) thỏa mãn đồng thời hai điều kiện
z
z
¯
+
4
-
3
i
và
z
+
1...
Đọc tiếp
Xét các số phức z = a + bi, (a,b ∈ R) thỏa mãn đồng thời hai điều kiện z = z ¯ + 4 - 3 i và z + 1 - i + z - 2 + 3 i đạt giá trị nhỏ nhất. Giá trị P = a + 2b là:
A. P = - 61 10
B. P = - 252 50
C. P = - 41 5
D. P = - 18 5
Xét các số phức
z
a
+
b
i
a
,
b
∈
ℝ
thỏa mãn đồng thời hai điều kiện
z
z
¯
+
4
-
3
i
và
z...
Đọc tiếp
Xét các số phức z = a + b i a , b ∈ ℝ thỏa mãn đồng thời hai điều kiện z = z ¯ + 4 - 3 i và z + 1 - i + z - 2 + 3 i đạt giá trị nhỏ nhất. Giá trị P = a + 2 b là:
A. P = - 252 50 .
B. P = - 41 5 .
C. P = - 61 10 .
D. P = - 18 5
Xét các số thực a, b thỏa mãn
a
b
1
. Tìm giá trị nhỏ nhất của biểu thức
P
log
a
b
2
a
2
+
3
log
b
a
b
A.
P...
Đọc tiếp
Xét các số thực a, b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 a 2 + 3 log b a b
A. P m i n = 19
B. P m i n = 13
C. P m i n = 14
D. P m i n = 15
Xét các số phức z a + bi, (a,b i) thỏa mãn |z – 3 – 3i| 6. Tính P 3a + b khi biểu thức 2|z + 6 – 3i| + |z + 1 + 5i| đạt giá trị nhỏ nhất. A. P
20
B. P
2
+
20
C. P
-
20
D. P
-
2
-
20
Đọc tiếp
Xét các số phức z = a + bi, (a,b i) thỏa mãn |z – 3 – 3i| = 6. Tính P = 3a + b khi biểu thức 2|z + 6 – 3i| + |z + 1 + 5i| đạt giá trị nhỏ nhất.
A. P = 20
B. P = 2 + 20
C. P = - 20
D. P = - 2 - 20
Cho số phức z thỏa mãn |z - 1 + 3i|+|z + 5 + i| 2
65
Giá trị nhỏ nhất của |z + 2 + i| đạt được khi z a + bi với a,b là các số thực dương. Giá trị của
2
a
2
+
b
2
bằng A. 17 B. 33 C. 24 D. 36
Đọc tiếp
Cho số phức z thỏa mãn
|z - 1 + 3i|+|z + 5 + i| = 2 65 Giá trị nhỏ nhất của
|z + 2 + i| đạt được khi z = a + bi với a,b là các số thực dương. Giá trị của 2 a 2 + b 2 bằng
A. 17
B. 33
C. 24
D. 36
15.Cho a, b, c là các số thực dương thỏa mãn a+b+c+ab+bc+ac6Chứng minh rằng: dfrac{a^3}{b}+dfrac{b^3}{c}+dfrac{c^3}{a}ge316. Xét các số thực a, b, c ( a khác 0) sao cho:Phương trình bậc hai ax^2+bx+c0 có hai nghiệm m, n thỏa mãn: 0le mle1;0le nle1.Tìm giá trị nhỏ nhất của biểu thức: Qdfrac{2a^2-ac-2ab+bc}{a^2-ab+ac}17. Cho ba số thực không âm a, b, c và thỏa amnx a+b+c1.Chứng minh rằng: a+2b+cge4left(1-aright)left(1-bright)left(1-cright)18.Cho ba số thực a, b, c. Chứng minh rằng: left(a^2-bcr...
Đọc tiếp
15.
Cho a, b, c là các số thực dương thỏa mãn \(a+b+c+ab+bc+ac=6\)
Chứng minh rằng: \(\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}\ge3\)
16.
Xét các số thực a, b, c ( a khác 0) sao cho:
Phương trình bậc hai \(ax^2+bx+c=0\) có hai nghiệm m, n thỏa mãn: \(0\le m\le1;0\le n\le1\).
Tìm giá trị nhỏ nhất của biểu thức: \(Q=\dfrac{2a^2-ac-2ab+bc}{a^2-ab+ac}\)
17.
Cho ba số thực không âm a, b, c và thỏa amnx a+b+c=1.
Chứng minh rằng: \(a+2b+c\ge4\left(1-a\right)\left(1-b\right)\left(1-c\right)\)
18.
Cho ba số thực a, b, c. Chứng minh rằng:
\(\left(a^2-bc\right)^3+\left(b^2-ca\right)^3+\left(c^2-ab\right)^3\ge3\left(a^2-bc\right)\left(b^2-ca\right)\left(c^2-ab\right)\)