Xét các hình chóp S.ABCD thỏa mãn các điều kiện: đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy và khoảng cách từ điểm A đến mặt phẳng S B C bằng a. Biết rằng thể tích khối chóp S.ABCD đạt giá trị nhỏ nhất V 0 khi cosin góc giữa đường thẳng SB và mặt phẳng A B C D bằng p q , trong đó p, q là các số nguyên dương và phân số p q là tối giản. Tính T = p + q V 0 .
A. T = 3 3 a 3
B. T = 6 a 3
C. T = 2 3 a 3
D. T = 5 3 2 a 3
Đáp án C.
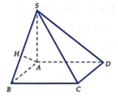
Ta có B C ⊥ A B ; B C ⊥ S A nên B C ⊥ S A B .
Gọi H là hình chiếu vuông góc của A trên SB.
Khi đó A H ⊥ S B C và d A , S B C = A H .
Ta có góc giữa đường thẳng SB và mặt phẳng A B C D là góc S B A ^ .
Đặt S B A ^ = α .
Theo giả thiết ta có A B = a sin α ; S A = a cos α .
Thể tích khối chóp S.ABCD là V = 1 3 . S A . S A B C D = 1 3 sin 2 α cos α a 3 .
Áp dụng bất đẳng thức Cô-si, ta có
sin 2 α . sin 2 α .2 cos 2 α ≤ sin 2 α + sin 2 α + 2 cos 2 α 3 3 = 8 27
Suy ra sin 2 α cos α ≤ 2 3 9 . Do đó V ≥ 3 2 a 3 .
Dấu bằng xảy ra khi sin 2 α = 2 cos 2 α ⇒ cos α = 1 3 .
Vậy thể tích khối chóp S.ABCD đạt giá trị nhỏ nhất bằng 3 2 a 3 khi cos α = 1 3 .
Suy ra V 0 = 3 2 a 3 ; p = 1, q = 3
⇒ T = p + q V 0 = 2 3 a 3 .



