Chọn đáp án C
*Trường hợp 1:
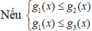
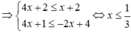
![]()
Do hàm số g 1 x = 4 x + 1 đồng biến trên ( - ∞ ; 1 3 ]
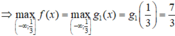
Chọn đáp án C
*Trường hợp 1:
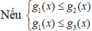
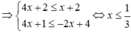
![]()
Do hàm số g 1 x = 4 x + 1 đồng biến trên ( - ∞ ; 1 3 ]
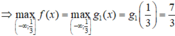
Cho hàm số y=f(x) nhận giá trị không âm và liên tục trên đoạn [0;1]. Đặt g ( x ) = 1 + 2 ∫ 0 x f ( t ) d t . Biết g ( x ) ≥ [ f ( x ) ] 3 với mọi x ∈ [ 0 ; 1 ] . Tích phân ∫ 0 1 [ g ( x ) ] 2 3 d x có giá trị lớn nhất bằng
A. 5 3
B. 4.
C. 4 3
D. 5.
Cho hàm số f(x)=(2 x +m)/(√x+1) với m là tham số thực, m>1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
A. 1
B. 3
C. 0
D. 2
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3
Cho hai hàm số y=f(x) và y=g(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số y=f’(x) là đường cong nét đậm, đồ thị hàm số y=g’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của y=f’(x) và y=g’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [a;c]

A. m i n h x a ; c = h 0
B. m i n h x a ; c = h a
C. m i n h x a ; c = h b
D. m i n h x a ; c = h c
Cho hàm số f(x) liên tục trên ℝ + thỏa mãn f ' x ≥ x + 1 x , ∀ x ∈ ℝ + và f(1) = 1. Tính giá trị nhỏ nhất của f(2).
A. 3
B. 2
C. 5 2 + ln 2
D. 4
Trên đoạn [1;4] các hàm số f ( x ) = x 2 + p x + q ; g ( x ) = x + 4 x 2 có cùng giá trị nhỏ nhất và đạt tại cùng một điểm. Hỏi giá trị lớn nhất của hàm số f(x) trên đoạn [1;4] là?
A. 4.
B. 7.
C. 11.
D. 9.
Cho hàm số y = f(x) có đạo hàm f ' x = x x + 1 x - 2 2 với mọi x ∈ ℝ . Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [-1 ;2] là
A. f(-1)
B. f(0)
C. f(3)
D. f(2)
Cho hai hàm số y=f(x), y=g(x) có đạo hàm là f '(x), g'(x). Đồ thị hàm số y=f '(x) và y=g(x) được cho như hình vẽ bên dưới.
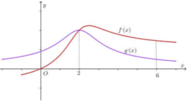
Biết rằng f 0 - f 6 < g 0 - g 6 . Giá trị lớn nhất, giá trị nhỏ nhất của hàm số h x = f x - g x trên đoạn 0 ; 6 lần lượt là:
A. h 2 ; h 6
B. h 6 ; h 2
C. h 0 ; h 2
D. h 2 ; h 0
Cho hàm số y = f ( x ) liên tục trên ℝ và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau
(1) Hàm số y = f ( x ) đạt cực đại tại x 0 = 0
(2) Hàm số y = f ( x ) có ba cực trị.
(3) Phương trình y = f ( x ) có đúng ba nghiệm phân biệt
(4) Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
Hỏi trong 4 mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 1
B. 3
C. 4
D. 2