Các câu hỏi tương tự
Với a,b,c > 0 Cm (a^2+b^2)c + (b^2 + c^2 )a + ( c^2 + a^2 )b > hoặc = 6abc
Với a,b,c >0 và a+b+c+ab+bc+ca=6abc. CMR: 1/a2+1/b2+1/c2 lớn hơn hoặc bằng 3
Với a,b,c là các số thực dương thỏa mãn: \(a+b+c+ab+bc+ca=6abc\).Chứng Minh Rằng:
\(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge3\)
1)Cho a,b,c >0
Chứng minh bc/a^2(b+c) + ca/b^2(c+a) +ab/c^2(a+b) > hoặc = 1/2(1/a+1/b+1/c)
2) Cho a,b,c>0 1/a + 1/b + 1/c =1
Chứng minh (b+c)/a^2 + (c+a)/b^2 + (a+b)/c^2 > hoặc = 2
cho các số dương a,b,c thỏa manc điều kiện a + b + c + ab + bc + ac = 6abc.
chứng minh rằng: \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge3\)
Cho a,b,c dương thỏa mãn a+b+c+ab+bc+ca=6abc
Chứng minh rằng \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge3\)
1Cho x,y >1 . Chứng minh : x2/(y-1) + y2/ (x-1) lớn hơn hoặc bằng 8
2 Cho a,b,c,d >=0 . Chứng minh : (a+b)(a+b+c)(a+b+c+d) / abcd lớn hơn hoặc bằng 64
3 Cho a,b,c >= 0 . Chứng minh : (a+b+c)(ab+bc+ac) lớn hơn hoặc bằng 8(a+b)(b+c)(c+a) / 9
4 Cho a,b,c >=0 và a+b+c =1 . Chứng minh : bc/√(a+bc) + ac/√(b+ac) + ab/√(c+ab) bé hơn hoặc bằng 1/2
Chứng minh rằng với a+b>c và |a-b|<c với a,b,c >0 thì phương trình bậc hai a^2x^2 +(a^2+b^2-c^2)x +b^2=0 vô nghiệm
ĐOẠN MK BÔI ĐỎ GIẢI THÍCH HỘ
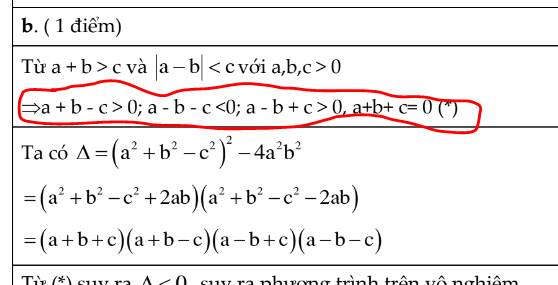
a) Chứng minh rằng với a, b , c là các số thực thì phương trình sau luôn có nghiệm:(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) 0b) Chứng minh rằng với ba số thức a, b , c phân biệt thì phương trình sau có hai nghiệm phân biết: c) Chứng minh rằng phương trình: c2x2 + (a2 – b2 – c2)x + b2 0 vô nghiệm với a, b, c là độ dài ba cạnh của một tam giác.d) Chứng minh rằng phương trình bậc hai:(a + b)2x2 – (a – b)(a2 – b2)x – 2ab(a2 + b2) 0 luôn có hai nghiệm phân biệt.
Đọc tiếp
a) Chứng minh rằng với a, b , c là các số thực thì phương trình sau luôn có nghiệm:
(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) = 0
b) Chứng minh rằng với ba số thức a, b , c phân biệt thì phương trình sau có hai nghiệm phân biết: 
c) Chứng minh rằng phương trình: c2x2 + (a2 – b2 – c2)x + b2 = 0 vô nghiệm với a, b, c là độ dài ba cạnh của một tam giác.
d) Chứng minh rằng phương trình bậc hai:
(a + b)2x2 – (a – b)(a2 – b2)x – 2ab(a2 + b2) = 0 luôn có hai nghiệm phân biệt.









