\(7=\dfrac{2^{10}.\left(3^2\right)^{41}.\left(5^2\right)^{23}}{3^{50}.\left(3.5\right)^{35}.\left(2.5\right)^9}=\dfrac{2^{10}.3^{82}.5^{46}}{3^{50}.3^{35}.5^{35}.2^9.5^9}\\ =\dfrac{2^{10}.3^{82}.5^{46}}{3^{85}.5^{44}.2^9}=\dfrac{2.5^2}{3^3}\\ =\dfrac{2.10}{27}=\dfrac{20}{27}\)
\(8=\dfrac{5^{62}.\left(2^4\right)^{15}}{\left(2^3\right)^{19}.\left(5^3\right)^{21}}=\dfrac{5^{62}.2^{60}}{2^{57}.5^{63}}=\dfrac{2^3}{5}=\dfrac{8}{5}\)
\(9=\dfrac{\left(2^2.5\right)^{12}.\left(2^3\right)^4.3^{14}}{\left(3.5\right)^{13}.2^{36}}=\dfrac{2^{24}.5^{12}.2^{12}.3^{14}}{3^{13}.5^{13}.2^{35}}\\ =\dfrac{2^{36}.5^{12}.3^{14}}{3^{13}.5^{13}.2^{35}}=\dfrac{2.3}{5}=\dfrac{6}{5}\)
\(10=\dfrac{\left(2^3\right)^{66}.\left(3^3\right)^{133}}{\left(3^2\right)^{99}.\left(2.3\right)^{200}}=\dfrac{2^{198}.3^{399}}{3^{198}.2^{200}.3^{200}}\\ =\dfrac{2^{198}.3^{399}}{3^{398}.2^{200}}=\dfrac{3}{2^2}=\dfrac{3}{4}\)
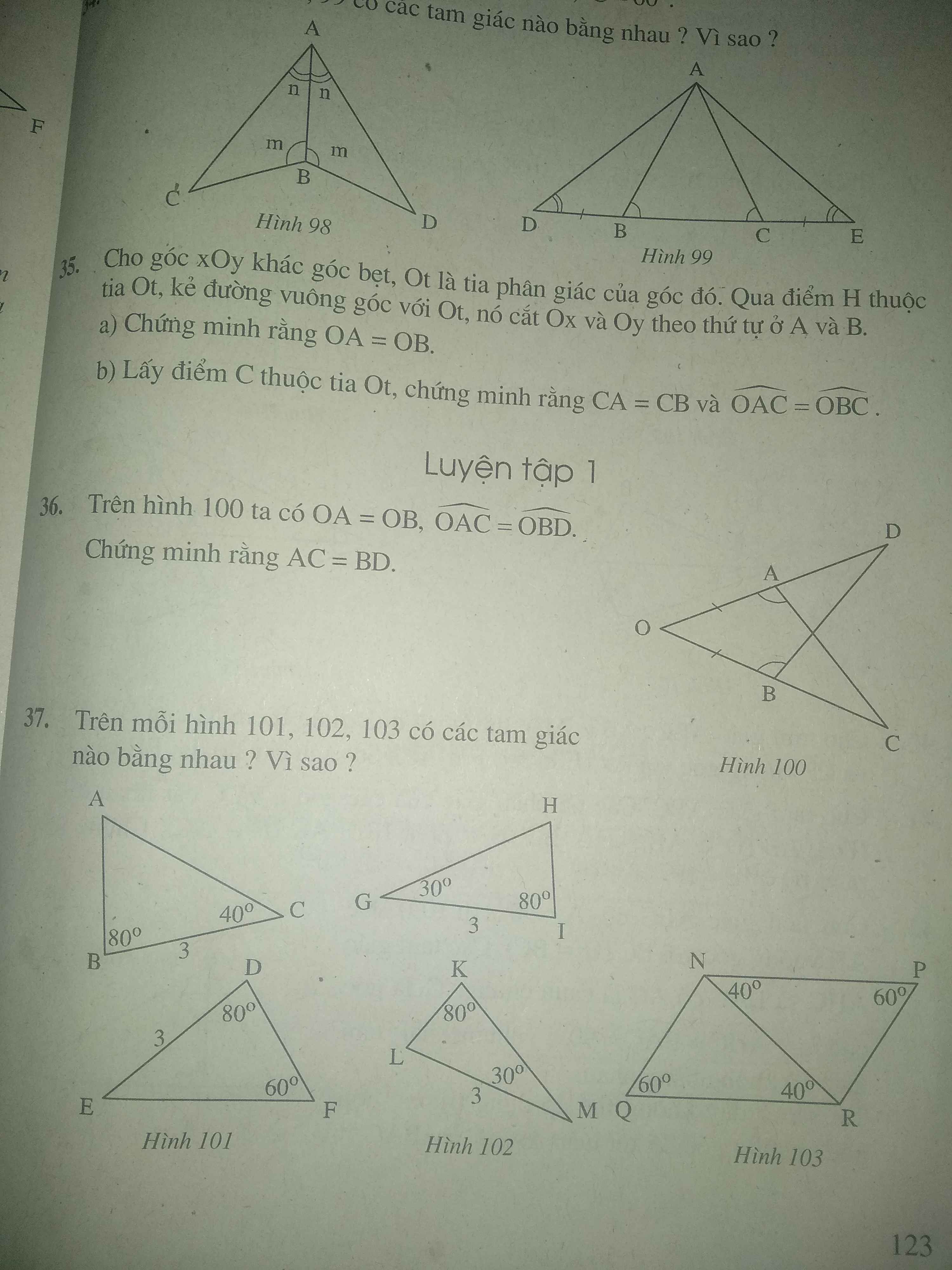
Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha 
)
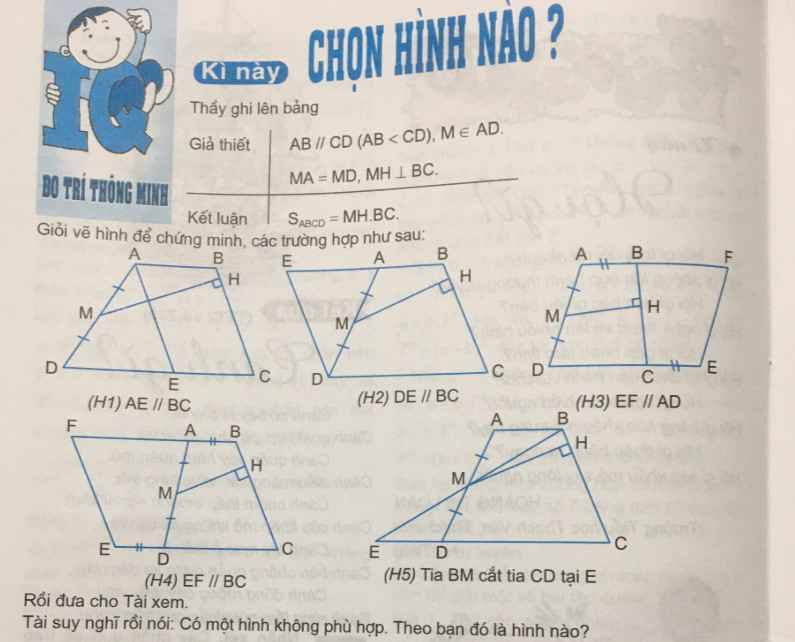
giải giúp e câu 4,5 có hình và lời giải chi tiết ạ !
