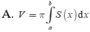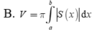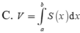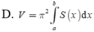Các câu hỏi tương tự
Viết công thức tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với Ox tại các điểm xa, xb (ab) có diện tích thiết diện bị cắt bởi hai mặt phẳng vuông với trục Ox tại điểm có hoành độ x (axb) là S(x)
Đọc tiếp
Viết công thức tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với Ox tại các điểm x=a, x=b (a<b) có diện tích thiết diện bị cắt bởi hai mặt phẳng vuông với trục Ox tại điểm có hoành độ x (a<x<b) là S(x)
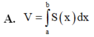
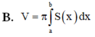
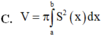
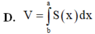
Cắt một vật thể (T) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại xa, xb (ab). Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x
a
≤
x
≤
b
cắt (T) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a;b]. Thể tích V của phần vật thể (T) giới hạn bởi mặt phẳng (P) và (Q) được cho bởi công thức nào dưới đây? A.
V...
Đọc tiếp
Cắt một vật thể (T) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại x=a, x=b (a<b). Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x a ≤ x ≤ b cắt (T) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a;b]. Thể tích V của phần vật thể (T) giới hạn bởi mặt phẳng (P) và (Q) được cho bởi công thức nào dưới đây?
A. V = ∫ a b S x d x
B. V = π ∫ a b S x d x
C. V = π 2 ∫ a b S x d x
D. V = π ∫ a b S 2 x d x
Cắt một vật thể (T) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại xa; xb. Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x cắt (T) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a;b]. Thể tích V của phần vật thể (T) giới hạn bởi mặt phẳng (P) và (Q) được cho bởi công thức nào dưới đây?
Đọc tiếp
Cắt một vật thể (T) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại x=a; x=b. Một mặt phẳng tùy ý vuông góc với trục Ox tại điểm x cắt (T) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a;b]. Thể tích V của phần vật thể (T) giới hạn bởi mặt phẳng (P) và (Q) được cho bởi công thức nào dưới đây?
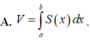
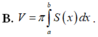
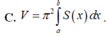
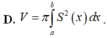
Trong không gian (Oxyz), cho vật thể (H) giới hạn bởi hai mặt phẳng có phương trình xa và xb (ba) Gọi S(x) là diện tích thiết diện của (H) bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x, với
a
≤
x
≤
b
Giả sử hàm số yS(x) liên tục trên đoạn [a;b]. Khi đó, thể tích V của vật thể (H) được cho bởi công thức:
Đọc tiếp
Trong không gian (Oxyz), cho vật thể (H) giới hạn bởi hai mặt phẳng có phương trình x=a và x=b (b<a) Gọi S(x) là diện tích thiết diện của (H) bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x, với a ≤ x ≤ b Giả sử hàm số y=S(x) liên tục trên đoạn [a;b]. Khi đó, thể tích V của vật thể (H) được cho bởi công thức:
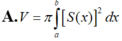

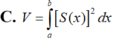
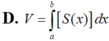
Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng x 0 và x 3, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x
0
≤
x
≤
3
là một hình chữ nhật có hai kích thước là x và
2
9
-
x
2
. A. 16 B. 17 C. 19 D. 18
Đọc tiếp
Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 3, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 3 là một hình chữ nhật có hai kích thước là x và 2 9 - x 2 .
A. 16
B. 17
C. 19
D. 18
Cho phần vật thể (T) giới hạn bởi hai mặt phẳng có phương trình x0 và x2. Cắt phần vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x, ta được thiết diện là một tam giác đều có độ dài cạnh bằng
x
2
-
x
. Tính thể tích V của phần vật thể (T).
Đọc tiếp
Cho phần vật thể (T) giới hạn bởi hai mặt phẳng có phương trình x=0 và x=2. Cắt phần vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x, ta được thiết diện là một tam giác đều có độ dài cạnh bằng x 2 - x . Tính thể tích V của phần vật thể (T).
![]()

![]()
![]()
Thể tích phần vật thể giới hạn bởi hai mặt phẳng x 0 và x 3 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(0 ≤ x ≤ 3) là một hình chữ nhật có hai kích thước là x và
2
(
9
-
x
2
)
A.
6
3
B. 18 C.
2
3...
Đọc tiếp
Thể tích phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 3 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(0 ≤ x ≤ 3) là một hình chữ nhật có hai kích thước là x và 2 ( 9 - x 2 )
A. 6 3
B. 18
C. 2 3 3
D. 3 3 3
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x1 và x4, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x (
1
≤
x
≤
4
) thì được thiết diện là một hình lục giác đều có độ dài cạnh là 2x.
Đọc tiếp
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x=1 và x=4, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x ( 1 ≤ x ≤ 4 ) thì được thiết diện là một hình lục giác đều có độ dài cạnh là 2x.
![]()
![]()
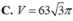
![]()
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x 1 và x 3, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và
3
x
2
-
2
Đọc tiếp
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và 3 x 2 - 2
![]()

![]()