Chọn D
Nếu S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox thì thể tích của vật thể giới hạn bởi hai mặt phẳng x = a và x = b là V = ∫ a b S x d x .
Chọn D
Nếu S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox thì thể tích của vật thể giới hạn bởi hai mặt phẳng x = a và x = b là V = ∫ a b S x d x .
Thể tích phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 3 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(0 ≤ x ≤ 3) là một hình chữ nhật có hai kích thước là x và 2 ( 9 - x 2 )
A. 6 3
B. 18
C. 2 3 3
D. 3 3 3
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và 3 x 2 - 2
![]()
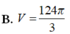

![]()
Cho vật thể giới hạn bởi hai mặt phẳng x = 0 ; x = π 2 , biết rằng thiết diện của vật thể khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 0 ≤ x ≤ π 2 ) là một hình tròn có bán kính R = cos x Thể tích của vật thể đó là
![]()
![]()
![]()
![]()
Cho phần vật thể (T) giới hạn bởi hai mặt phẳng có phương trình x=0 và x=2. Cắt phần vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x, ta được thiết diện là một tam giác đều có độ dài cạnh bằng x 2 - x . Tính thể tích V của phần vật thể (T).
![]()

![]()
![]()
Tính thể tích vật thể giới hạn bởi hai mặt phẳng x = 0 , x = π . Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác vuông cân có cạnh huyền bằng sin x + 2 .
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0, x = 2, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 2 là một nủa hình tròn đường kính 5 x 2 .
A. 4 π
B. π
C. 3 π
D. 2 π
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = 3 , biết thiết diện của vật thể cắt bởi mặt phẳng (P) vuông góc với trục tại điểm có hoành độ x ( 0 ≤ x ≤ 3 ) là một hình chữ nhật có độ dài hai cạnh là x và 1 + x 2
A. 1
B. 2
C. 7/3
D. 3
Viết công thức tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với Ox tại các điểm x=a, x=b (a<b) có diện tích thiết diện bị cắt bởi hai mặt phẳng vuông với trục Ox tại điểm có hoành độ x (a<x<b) là S(x)
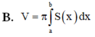
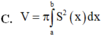
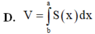
Tính thể tích V của vật thể giới hạn bởi hai mặt phẳng x=0 và x=4 , biết rằng khi cắt bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x(0<x<4) thì được thiết diện là nửa hình tròn bán kính R = x 4 - x
![]()
![]()
![]()
![]()