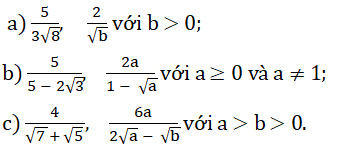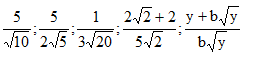\(\sqrt{A^2}=\left|A\right|\)
\(\sqrt{A_1\cdot A_2\cdot...\cdot A_n}=\sqrt{A_1}\cdot\sqrt{A_2}\cdot...\cdot\sqrt{A_n}\)(ĐK: \(A_1>=0;A_2>=0;...;A_n>=0\))
\(\sqrt{\dfrac{A}{B}}=\dfrac{\sqrt{A}}{\sqrt{B}}\left(A>=0;B>0\right)\)
\(\sqrt{\dfrac{A}{B}}=\sqrt{\dfrac{AB}{B^2}}=\dfrac{\sqrt{AB}}{B}\left(A>=0;B>0\right)\)
\(\sqrt{A^2\cdot B}=\left|A\right|\cdot\sqrt{B}\left(B>=0\right)\)
\(A\cdot\sqrt{B}=\left[{}\begin{matrix}\sqrt{A^2\cdot B}\left(A>=0\right)\\-\sqrt{A^2\cdot B}\left(A< 0\right)\end{matrix}\right.\)