Vì các dây cung AB = BC = CD = DE = EF = FA bằng nhau nên khoảng cách từ O đến các dây là bằng nhau ( định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây)
a) Vẽ đường tròn tâm O bán kính R = 2cm.
b) Vẽ một lục giác đều ABCDEF có tất cả các đỉnh nằm trên đường tròn (O).
c) Vì sao tâm O cách đều các cạnh của lục giác đều ? Gọi khoảng cách này là r.
d) Vẽ đường tròn (O; r).
Cho hình lục giác đều cạnh a. Gọi M là một điểm bất kù trong hình lục giác và d là tổng khoảng cách từ điểm M đến các cạnh của hình lục giác.
a, Chứng minh rằng d không phụ thuộc vào vị trí của M
b, Tính d theo a
Cho đường tròn (O;R) và 1 điểm A cách O 1 khoảng 2R. Từ A vẽ các tiếp tuyến AB,AC với đường tròn (B,C là các tiếp điểm)
a) Cm: OA là đường trung trực của BC
b) Gọi H là giao điểm của OA và BC. Cm: HA.HO=HB.HC
c)Cm: tam giác ABC đều. Tính cạnh AB theo R
d) OA cắt đường tròn (O) tại I. Cm: I là tâm đường tròn nội tiếp tam giác
Giúp mình giải câu d nhé !!!!!!!!!!!!!
Nhờ mọi người giải giúp mình bài toán này:
Cho ngũ giác đều ABCDE cạnh a, gọi M là điểm bất kỳ trong hình ngũ giác đều. Gọi d là tổng các khoảng cách từ M đến các cạnh của hình ngũ giác.
a) Chứng minh rằng d không phụ thuộc vào vị trí M
b) Tính d theo a
Cho tam giác đều \(ABC\) có độ dài cạnh bằng \(a\). Gọi \(M\) là 1 điểm nằm trong tam giác. \(MI,MP,MQ\) theo thứ tự là khoảng cách từ \(M\) đến các cạnh \(BC,AB,AC\). Gọi \(O\) là trung điểm của cạnh \(BC\). Các điểm \(D\) và \(E\) theo thứ tự chuyển động trên các cạnh \(AB\) và \(AC\) sao cho \(\widehat{DOE}=60^o\).
\(a\)) Chứng minh: \(MI+MP+MQ\) không đổi.
\(b\)) Chứng minh: Đường thẳng \(DE\) luôn tiếp xúc với một đường tròn cố định.
\(c\)) Xác định vị trí của \(D\) và \(E\) để diện tích tam giác \(DOE\) đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó theo \(a\).
cho hình lục giác đều abcdef cạnh a. Cho 1 điểm M bất kì trong hình lục giác. Gọi d là tổng các khoản cách từ điểm M đến các cạnh của hình lục giác
a. cm rằng d ko phụ thuộc vào vị trí của điểm M
b. tính d theo a nhỏ
Cho tam giác ABC đều có cạnh bằng a. Gọi O là trung điểm của BC. Một góc xOy bằng 60o quay quanh điểm O sao cho hai cạnh Ox, Oy luôn cắt AB và AC lần lượt tại M và N.
a) cm: Tam giác OBM đồng dạng với tam giác NCO.
b) cm: BC2=4BM.CN.
c) Khoảng cách từ điểm O đến MN không đổi khi Ox; Oy thay đổi.
d) Từ O vẽ đường thẳng d bất kì cắt AB; AC tại P; Q.
CMR: \(\dfrac{1}{AP}+\dfrac{1}{AQ}\) không đổi.
Vẽ hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.
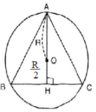
Vẽ hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.
