a.
Do AM là trung tuyến \(\Rightarrow BM=CM\)
Xét hai tam giác AMB và DMC có:
\(\left\{{}\begin{matrix}MA=MD\left(gt\right)\\\widehat{AMB}=\widehat{DMC}\left(\text{đối đỉnh}\right)\\BM=CM\end{matrix}\right.\)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
\(\Rightarrow AB=CD\)
b.
Từ \(\Delta AMB=\Delta DMC\Rightarrow\widehat{ABM}=\widehat{DCM}\)
Mà \(\widehat{ABM}+\widehat{ACM}=90^0\) (do tam giác ABC vuông tại A)
\(\Rightarrow\widehat{ACM}+\widehat{DCM}=90^0\)
\(\Rightarrow\widehat{ACD}=90^0\)
\(\Rightarrow DC\perp AC\)

 vẽ hình giúp e vs ạ
vẽ hình giúp e vs ạ

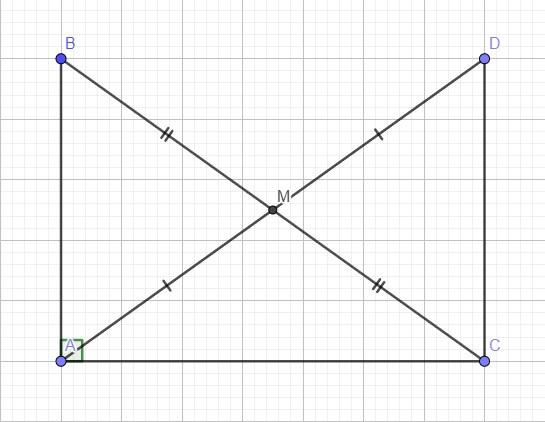














 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn