Bài 1:
a, H là trung điểm của BC ⇒ BH = CH
Xét tam giác ABH và tam giác ACH có:
AB = AC
AH chung
BH = CH
⇒ ΔABH = Δ ACH (c-c-c) (dpcm)
b, Do ΔABH = Δ ACH ⇒ \(\widehat{AHB}=\widehat{AHC}\) (2 góc tương ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^o\) (do 2 góc kề bù)
\(\Rightarrow\widehat{AHB}+\widehat{AHB}=180^o\)
\(\Rightarrow2\widehat{AHB}=180^o\)
\(\Rightarrow\widehat{AHB}=180^o:2=90^o\) \(\Rightarrow AH\perp HB\) hay \(AH\perp BC\left(dpcm\right)\)
Bài 2: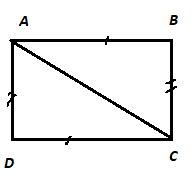
a, Xét tam giác ABC và tam giác CDA có:
AB = CD
AC chung
AD = BC
⇒ ΔABC = ΔCDA (c-c-c) (dpcm)
b, Do ΔABC = ΔCDA ⇒ \(\widehat{BCA}=\widehat{DAC},\widehat{BAC}=\widehat{DCA}\) (cặp góc tương ứng)
mà: \(\widehat{BCA},\widehat{DAC}\) là 2 góc ở vị trí so le trong ⇒ BC//AD (dpcm)
\(\widehat{BAC},\widehat{DCA}\) là 2 góc ở vị trí so le trong ⇒ AB // CD (dpcm)




