Bài 5:
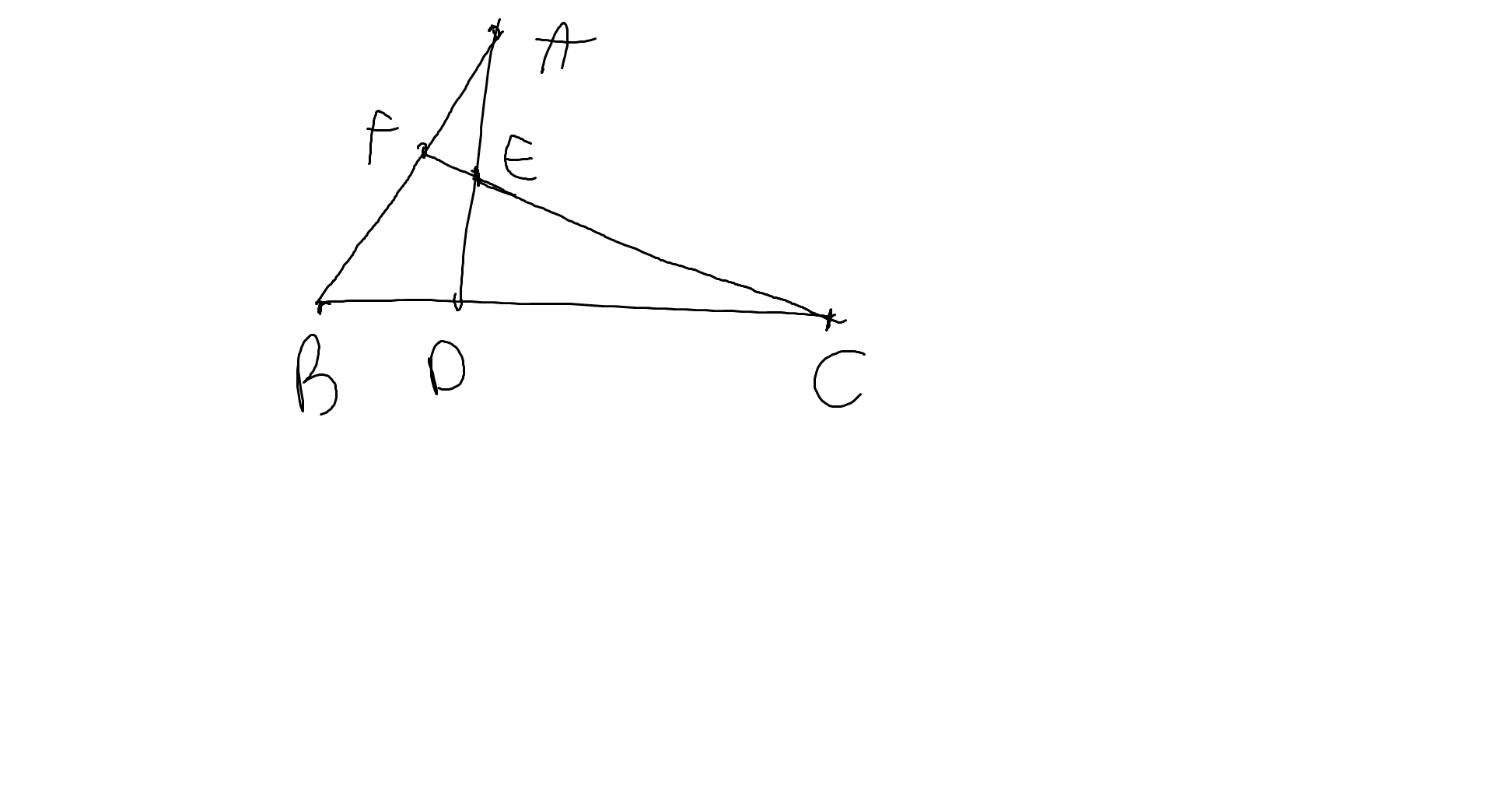
a: Xét ΔADB vuông tại D và ΔCDE vuông tại D có
DA=DC
DB=DE
Do đó ΔADB=ΔCDE
=>AB=CE
b: ΔADB=ΔCDE
=>\(\widehat{ABD}=\widehat{CED}\)
mà \(\widehat{CED}+\widehat{ECD}=90^0\)(ΔEDC vuông tại D)
nên \(\widehat{FBC}+\widehat{FCB}=90^0\)
=>CF\(\perp\)AB
Bài 6:
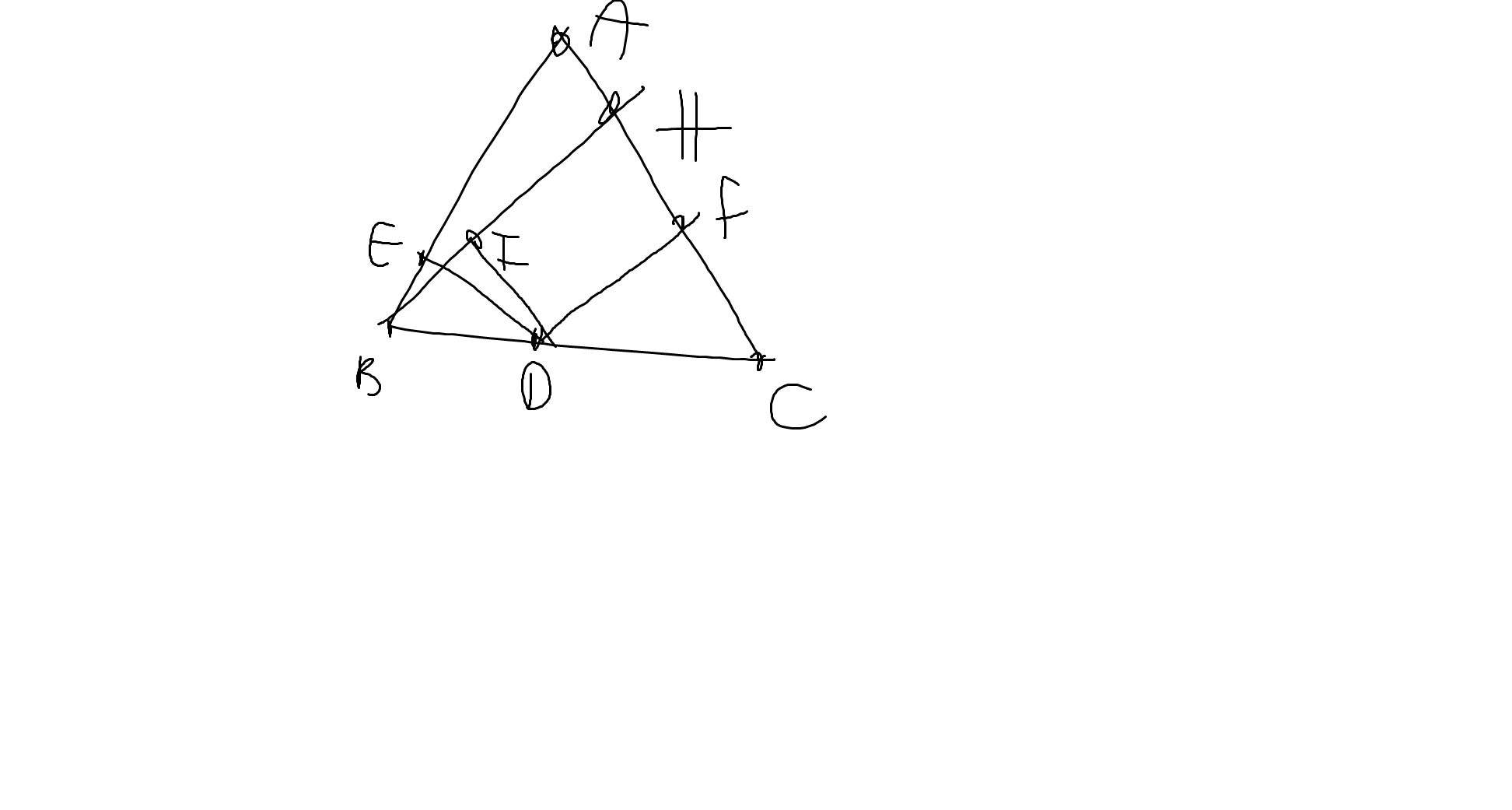
Ta có: DF\(\perp\)AC
BH\(\perp\)AC
Do đó: DF//BH
Xét ΔIDH và ΔFHD có
\(\widehat{IDH}=\widehat{FHD}\)(hai góc so le trong, ID//FH)
DH chung
\(\widehat{IHD}=\widehat{FDH}\)(hai góc so le trong, IH//FD)
Do đó: ΔIDH=ΔFHD
=>IH=FD
Ta có: ID//AC
=>\(\widehat{IDB}=\widehat{ACB}\)
mà \(\widehat{ACB}=\widehat{ABC}\)(gt)
nên \(\widehat{IDB}=\widehat{ABC}\)
Ta có: DI//AC
AC\(\perp\)BH
Do đó: DI\(\perp\)BH tại I
Xét ΔEBD vuông tại E và ΔIDB vuông tại I có
BD chung
\(\widehat{EBD}=\widehat{IDB}\)
Do đó: ΔEBD=ΔIDB
=>DE=BI
DE+DF=BI+IH=BH
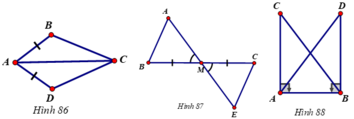
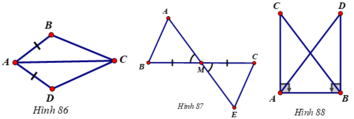
Bài 7:
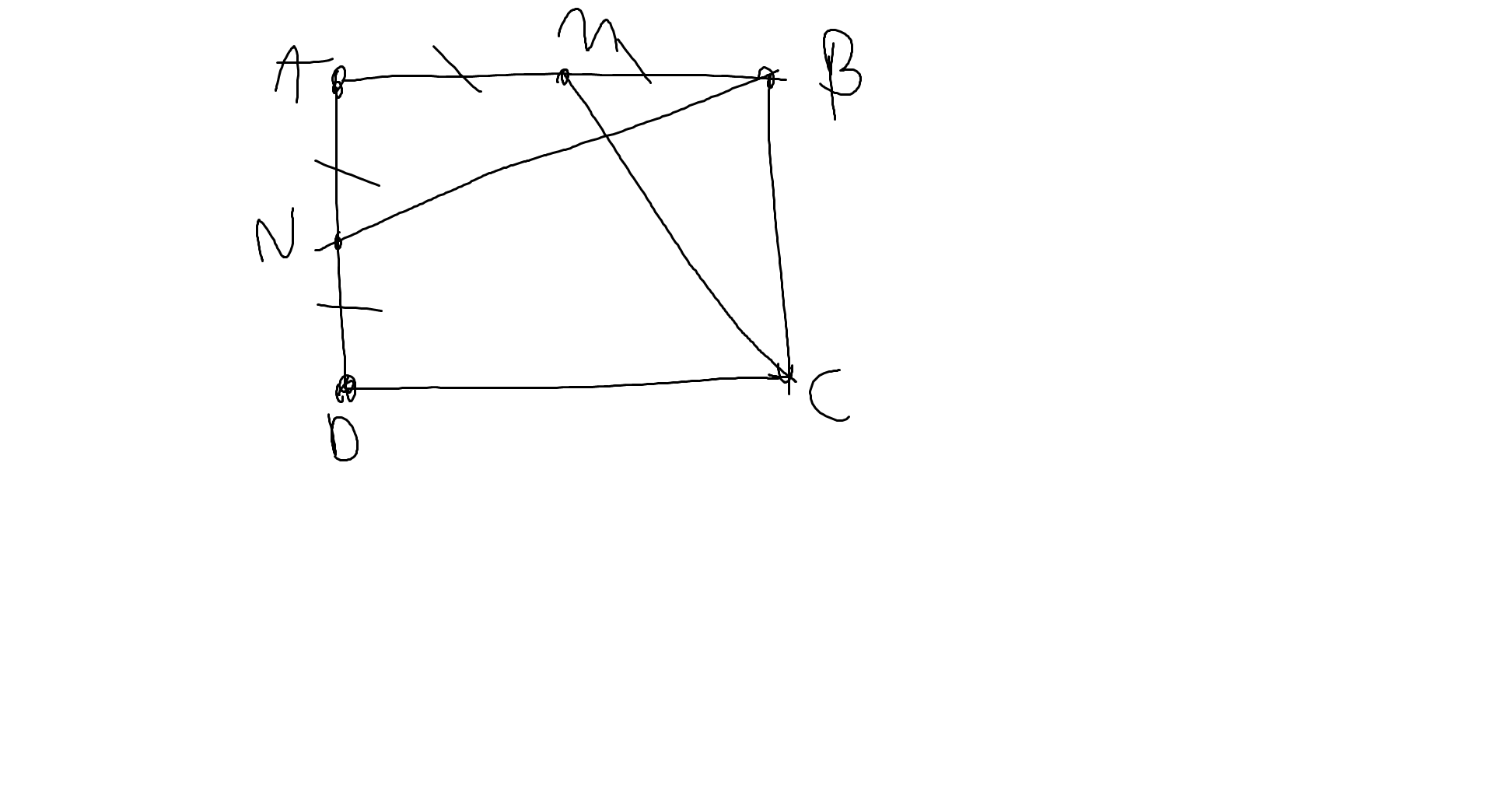
Ta có: \(AN=ND=\dfrac{AD}{2}\)
\(AM=MB=\dfrac{AB}{2}\)
mà AD=AB
nên AN=ND=AM=MB
Xét ΔBAN vuông tại A và ΔCBM vuông tại B có
BA=CB
AN=BM
Do đó: ΔBAN=ΔCBM
=>\(\widehat{ABN}=\widehat{BCM}\)
=>\(\widehat{ABN}+\widehat{BMC}=90^0\)
=>MC\(\perp\)BN
Ta có: ΔBAN=ΔCBM
=>BN=MC