Bài 3:
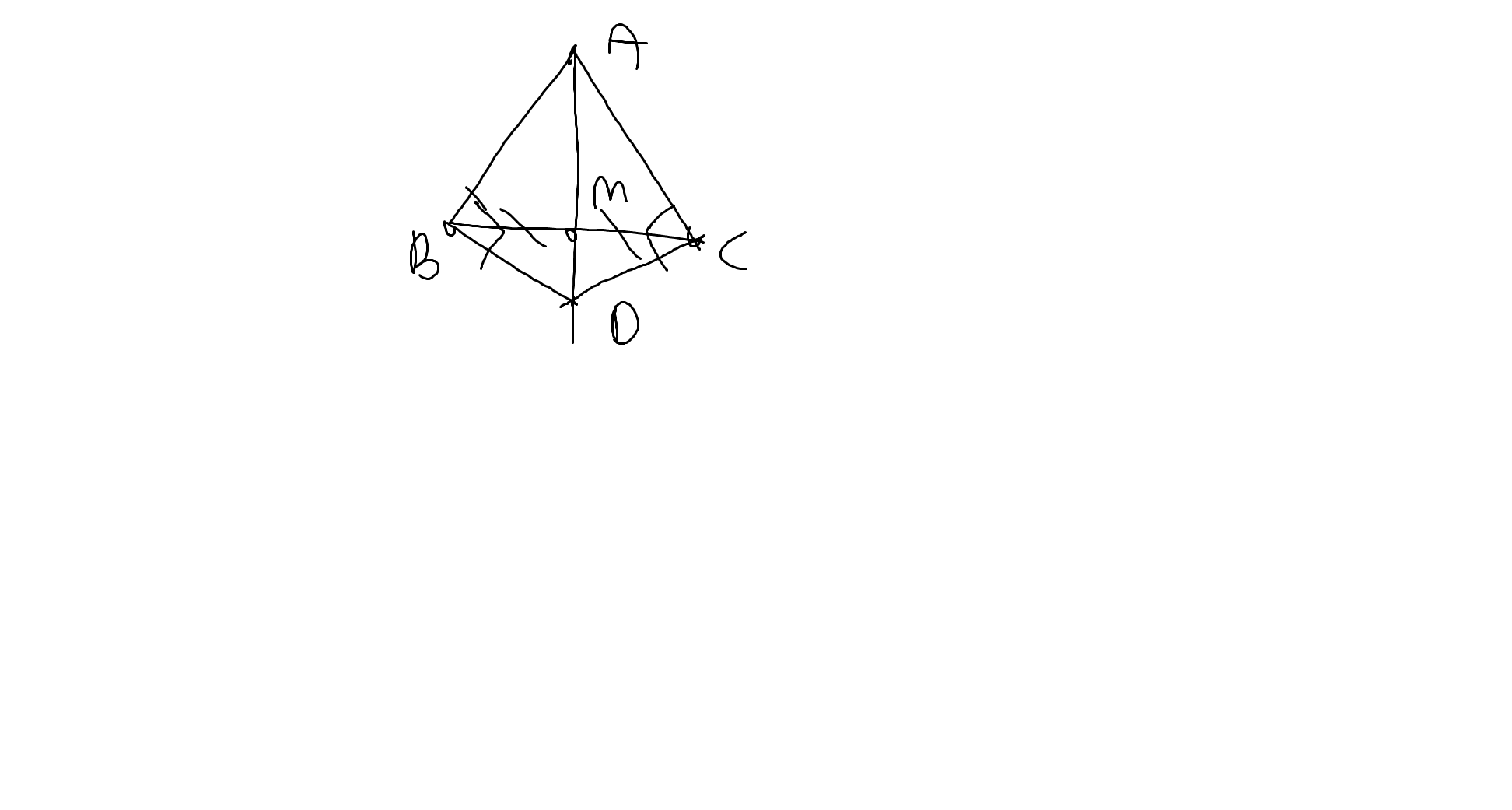
a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD
=>\(\widehat{BAD}=\widehat{CAD}\)
=>AD là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là phân giác của \(\widehat{BAC}\)
mà AD là phân giác của \(\widehat{BAC}\)
và AM,AD có điểm chung là A
nên A,M,D thẳng hàng
Bài 4:
a: Ta có: \(\widehat{MAB}+\widehat{BAC}+\widehat{CAN}=180^0\)
=>\(\widehat{MAB}+\widehat{CAN}+90^0=180^0\)
=>\(\widehat{MAB}+\widehat{CAN}=180^0-90^0=90^0\)
mà \(\widehat{MAB}+\widehat{MBA}=90^0\)
nên \(\widehat{MBA}=\widehat{NAC}\)
XétΔMBA vuông tại M và ΔNAC vuông tại N có
BA=AC
\(\widehat{MBA}=\widehat{NAC}\)
Do đó: ΔMBA=ΔNAC
b: ΔMBA=ΔNAC
=>MB=NA; MA=NC
Ta có: MA+AN=MN
mà MA=NC và MB=NA
nên NC+MB=MN